Question

【题目】如图，在△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH、BE与相交于点G，以下结论中正确的结论有（ ） （1.）△ABC是等腰三角形 （2.）BF=AC
（3.）BH：BD：BC=1： （4.）GE2+CE2=BG2 ．

A.1个
B.2个
C.3个
D.4个

Answer 1

【答案】C
【解析】解：（1.）∵BE平分∠ABC，∴∠ABE=∠CBE，
∵CD⊥AB，
∴∠ABE+∠A=90°，∠CBE+∠ACB=90°，
∴∠A=∠BCA，
∴AB=BC，
∴△ABC是等腰三角形；
故（1）正确；
（2.）∵CD⊥AB，BE⊥AC，
∴∠BDC=∠ADC=∠AEB=90°，
∴∠A+∠ABE=90°，∠ABE+∠DFB=90°，
∴∠A=∠DFB，
∵∠ABC=45°，∠BDC=90°，
∴∠DCB=90°﹣45°=45°=∠DBC，
∴BD=DC，
在△BDF和△CDA中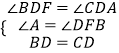
，
∴△BDF≌△CDA（AAS），
∴BF=AC；
故（2）正确；
（3.）∵在△BCD中，∠CDB=90°，∠DBC=45°，
∴∠DCB=45°，
∴BD=CD，BC= BD．
由点H是BC的中点，
∴DH=BH=CH= BC，
∴BD= BH，
∴BH：BD：BC=BH： BH：2BH=1： ：2．
故（3）错误；
（4.）由（2）知：BF=AC，
∵BF平分∠DBC，
∴∠ABE=∠CBE，
又∵BE⊥AC，
∴∠AEB=∠CEB，
在△ABE与△CBE中，
，
∴△ABE≌△CBE（AAS），
∴CE=AE= AC，
∴CE= AC= BF；
连接CG．
∵BD=CD，H是BC边的中点，
∴DH是BC的中垂线，
∴BG=CG，
在Rt△CGE中有：CG2=CE2+GE2 ，
∴CE2+GE2=BG2 ．
故（4）正确．
综上所述，正确的结论由3个．
故选：C．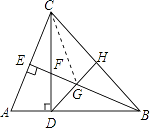

【考点精析】本题主要考查了勾股定理的概念的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．