【题目】如图,四边形ABCD是平行四边形,∠BAD的平分线交BD于点E , 交CD于点F , 交BC的延长线于点G , 则下列结论中正确的是( ) 
A.AE2=EFFG
B.AE2=EFEG
C.AE2=EGFG
D.AE2=EFAG
参考答案:
【答案】B
【解析】解答:∵四边形ABCD是平行四边形,∴△ADE∽△EGB , △DEF∽△AEB ,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
即AE2=EFEG .
所以选项B正确,
故选B .
分析:解答此题的关键是利用平行四边形证明出△ADE∽△EGB , △DEF∽△AEB , 然后利用对应边成比例即可解答此题.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D , E分别在AB , AC上,DE∥BC , AD=CE . 若AB:AC=3:2,BC=10,则DE的长为( )

A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
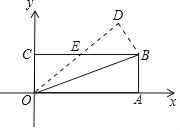
A.
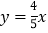 B.
B. 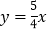 C.
C. 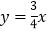 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为CD上一点,连接AE、BD , 且AE、BD交于点F , DE:EC=2:3,则S△DEF:S△ABF=( )
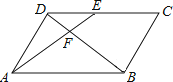
A.2:3
B.4:9
C.2:5
D.4:25 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC于D , 下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③
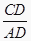 =
= 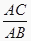 ;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( )
;④AB2=BDBC . 其中一定能够判定△ABC是直角三角形的有( ) 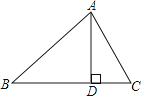
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,DE∥BC交AC于E , AD:DB=1:2,则△ADE与△ABC的面积之比为( )

A.1:2
B.1:4
C.1:8
D.1:9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使得△MNP为等腰直角三角形,则符合条件的点P有(提示:直角三角形斜边上的中线等于斜边的一半)( )

A. 2个 B. 3个 C. 4个 D. 5个
相关试题

