【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
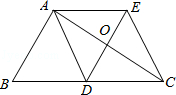
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
参考答案:
【答案】见解析
【解析】
试题分析:(1)先证四边形ABDE是平行四边形,再证四边形ADCE是平行四边形,即得AD=CE;
(2)由∠BAC=90°,AD是边BC上的中线,即得AD=BD=CD,结合(1)知四边形ADCE是平行四边形,即证;
证明:(1)∵DE∥AB,AE∥BC,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD
又∵AD是BC边的中线,
∴BD=CD,
∴AE=CD,
∵AE∥CD,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A′B′C′,∠A=20°,∠C=120°,则∠B′的度数为( )
A.20°
B.30°
C.40°
D.120° -
科目: 来源: 题型:
查看答案和解析>>【题目】如果△ABC∽△A′B′C′,BC=3,B′C′=1.8,则△A′B′C′与△ABC的相似比为( )
A.5:3
B.3:2
C.2:3
D.3:5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).
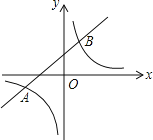
(1)求一次函数和反比例函数的表达式及点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2,;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣x+1的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】美国航空航天局发布消息,2011年3月19日,月球将到达19年来距离地球最近的位置,它与地球的距离约为356000千米,其中356000用科学记数法表示为 ( )
A. 3.56×105 B. 0.356×106 C. 3.56×104 D. 35.6×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】某印刷厂3月份印刷了50万册书籍,5月份印刷了72万册书籍,如果每月印刷的增长率都为x,则根据题意,可建立关于x的方程是_____.
相关试题

