【题目】如图,在ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.
(1)若∠CAE=∠B+30°,求∠B的大小;
(2)若AC=3,AB=5,求△AEB的周长.

参考答案:
【答案】(1)∠B=20°;(2)△AEB的周长=11.25.
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,根据等边对等角可得∠B=∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CEA=∠B+∠BAE=2∠B,然后在△ACE中,根据直角三角形两锐角互余列出方程求解即可;
(2)利用勾股定理列式求出BC=4,设AE=BE=x,表示出CE=4﹣x,然后在Rt△ACE中,利用勾股定理列式求出x,再根据三角形的周长的定义列式计算即可得解.
解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠BAE,
∴∠CEA=∠B+∠BAE=2∠B,
在△ACE中,∠CAE+∠CEA=∠B+30°+2∠B=90°,
解得∠B=20°;
(2)由勾股定理得,![]() =4,
=4,
设AE=BE=x,则CE=4﹣x,
在Rt△ACE中,AC2+CE2=AE2,
即32+(4﹣x)2=x2,
解得x=![]() ,
,
∴△AEB的周长=![]() ×2+5=11.25.
×2+5=11.25.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同.
(1)判断下列甲乙两人的说法,认为对的在后面括号内答“√”,错的打“×”.
甲:“从箱子里摸出一个球是白球或者红球”这一事件是必然事件;
乙:从箱子里摸出一个球,记下颜色后放回,搅匀,这样连续操作三次,其中必有一次摸到的是白球;
(2)小明说:从箱子里摸出一个球,不放回,再摸出一个球,则“摸出的球中有白球”这一事件的概率为 ,你认同吗?请画树状图或列表计算说明.
,你认同吗?请画树状图或列表计算说明. -
科目: 来源: 题型:
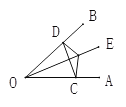
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数图象交x轴于点(-2,0),与y轴的交点到原点的距离为5,则该一次函数解析式为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆小汽车在高速公路上从静止到起动10秒内的速度经测量如下表:

(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用T表示时间,V表示速度,那么随着T的变化,V的变化趋势是什么?
(3)当T每增加1秒,V的变化情况相同吗?在哪1秒钟,V的增加最大?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各内角的度数是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′.若边A′B交线段CD于H,且BH=DH,则DH的值是( )

A.
B.
C.
D.
相关试题

