【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).

参考答案:
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接AC,再利用勾股定理列式求出AB2、BC2、AC2,然后利用勾股定理逆定理解答;
(2)根据勾股定理的逆定理判定△ABC是等腰直角三角形,根据全等三角形的判定和性质,可得结果.
解:(1)![]() ,
,
理由:如图①,连接![]() ,
,
由勾股定理可得![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() 是直角三角形且
是直角三角形且![]() ,
,
所以![]() ,
,

(2)![]() .
.
理由:如图②,连接AB 、BC,
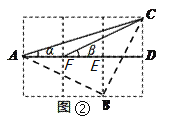
由勾股定理得![]() ,
,
![]() ,
,
![]() ,
,
所以![]() ,
,
所以![]() 是直角三角形且
是直角三角形且![]() .
.
又因为![]() ,所以
,所以![]() 是等腰直角三角形,
是等腰直角三角形,
∴∠CAB=45°,
在△ABE和△FCD中,
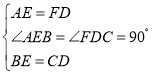 ,
,
∴△ABE≌△FCD(SAS),
∴∠BAD=∠β,
∴∠α+∠β=∠CAD+∠BAD=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.

(1)求FG的长;
(2)直接写出图中与△BHG相似的所有三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是长方形,∠A=∠ABC=∠BCD=∠CDA=90°,AB∥CD,AD∥BC,E是边AD上一动点.
(1)若∠ECD=2∠ECB,求∠AEC的度数.
(2)若∠ABD=70°,△DEF是等腰三角形,求∠ECB的度数.
(3)若△EFD的面积为4,若△DCF的面积为6,则四边形ABFE的面积为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
(1)求BE的长度;
(2)求△ABE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,
中, ,
, 为
为 上一动点,
上一动点, 交
交 于
于 ,过
,过 作
作 交
交 于
于 ,连接
,连接 ,过
,过 作
作 于
于 ,下列有四个结论:①
,下列有四个结论:① ,②
,② ,③
,③ ,④
,④ 的周长为定值,其中正确的结论有( ).
的周长为定值,其中正确的结论有( ).
A.①②③B.①②④C.①③④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
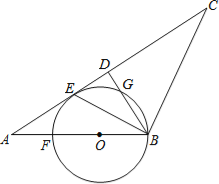
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
相关试题

