【题目】如图,四边形ABCD是长方形,∠A=∠ABC=∠BCD=∠CDA=90°,AB∥CD,AD∥BC,E是边AD上一动点.
(1)若∠ECD=2∠ECB,求∠AEC的度数.
(2)若∠ABD=70°,△DEF是等腰三角形,求∠ECB的度数.
(3)若△EFD的面积为4,若△DCF的面积为6,则四边形ABFE的面积为_______.

参考答案:
【答案】(1)∠AEC=150°;(2)20°或80°;(3)11.
【解析】
(1)由∠ECD=2∠ECB和∠BCD=90°可得:∠ECD=60o,∠BCE=30o,再由平行线的性质可得到∠AEC=150°;
(2)由∠ABD=70o得到∠ADB=20o,当EF=DF时,∠DEF=20o;当DE=DF时,∠DEF=80o,再由平行线的性质得到∠ECB=∠DEF;
(3) 由在矩形ABCD中,△EFD的面积为4,△FCD的面积为6,根据等高三角形的面积比等于对应底的比,即可求得EF:FEC,易得△DEF∽△BEC,然后由相似三角形面积比等于相似比的平方,即可求得△BFC的面积,继而求得答案.
(1)∵∠ECD=2∠ECB和∠BCD=90°,
∴∠ECD=60o,∠BCE=30o,
又∵AD//BC,
∴∠AEC+∠BCE=180o,
∴∠AEC=150°;
(2)∵∠ABD=70o,∠A=90o,
∴∠ADB=20o,
又∵△DEF是等腰三角形,
∴DE=DF或EF=DF,
当EF=DF时,∠FED=∠EDF=20o,
当DE=DF时,∠DEF=80o,
又∵AD//BC,
∴∠EBC=∠DEF,
∴∠EBC=20o或80o;
(3) ∵△EFD的面积为4,△FECD的面积为6,
∴EF:FC=4:6=2:3,
∵四边形ABCD是矩形,
∴AD∥BC,
∴△DEF∽△BFC,
∴S△DEF:S△BFC=(![]() )2=4:9,
)2=4:9,
∴S△BFC=9,
∴S△ABD=S△BCD=S△BFC+S△CDE=15,
∴S阴影=S△ABD-S△DEF=15-4=11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的对角线
的对角线 相交于点
相交于点 .
.
(1)求证:四边形
 为菱形;
为菱形;(2)
 垂直平分线段
垂直平分线段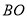 于点
于点 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.

(1)求FG的长;
(2)直接写出图中与△BHG相似的所有三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,
 ,
, ,
, 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)如图②,连接三格和两格的对角线,求
 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
(1)求BE的长度;
(2)求△ABE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,
中, ,
, 为
为 上一动点,
上一动点, 交
交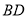 于
于 ,过
,过 作
作 交
交 于
于 ,连接
,连接 ,过
,过 作
作 于
于 ,下列有四个结论:①
,下列有四个结论:① ,②
,② ,③
,③ ,④
,④ 的周长为定值,其中正确的结论有( ).
的周长为定值,其中正确的结论有( ).
A.①②③B.①②④C.①③④D.①②③④
相关试题

