【题目】百货商店服装专柜在销售中发现:某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.为占有市场份额,在确保盈利的前提下.
(1)降价多少元时,每星期盈利为6125元.
(2)降价多少元时,每星期盈利额最大,最大盈利额是多少?
参考答案:
【答案】
(1)解:设降价x元时,每星期盈利为6125元,
根据题意,得:(20﹣x)(300+20x)=6125,
解得:x=2.5,
答:降价2.5元时,每星期盈利为6125元
(2)解:设降价x元时,每星期的盈利为y元,
则y=(60﹣x)(300+20x)﹣40(300+20x)=﹣20x2+100x+6000.
因为降价要确保盈利,所以40<60﹣x≤60,
解得:0≤x<20,
∴当x= ![]() =2.5时,y有最大值
=2.5时,y有最大值 ![]() =6125,
=6125,
答:当降价2.5元时,利润最大且为6125元
【解析】(1)设降价x元时,每星期盈利为6125元,根据:每件利润×销售量=总利润,列方程求解可得;(2)根据:利润=单件利润×售出的总件数列出函数表达式,根据x=﹣ ![]() 时,y有最大值.
时,y有最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从
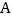 地出发,在南北方向的路上检修线路,如果规定向北行驶为正,向南行驶为负,一天行驶记录如下:(单位:千米)
地出发,在南北方向的路上检修线路,如果规定向北行驶为正,向南行驶为负,一天行驶记录如下:(单位:千米)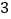 ,
,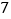 ,
,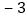 ,
,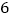 ,
,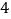 ,
,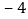 ,
,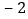 ,
,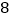 ,
,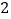 ,
,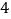 ,
,通过列式计算:
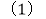 收工时检修工人离
收工时检修工人离 地多远?在
地多远?在 地的哪个方向上?
地的哪个方向上? 若检修人员用的是耗油为每千米
若检修人员用的是耗油为每千米 升的汽车作交通工具,那么这天中,这辆汽车共耗油多少升?
升的汽车作交通工具,那么这天中,这辆汽车共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在坐标系中作出旋转中心S并写出旋转中心S的坐标:S
(4)在x轴上有一点P,使得PA+PB的值最小,请作图标出P点并写出点P的坐标.P . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
 B.
B.  C. 4 D. 8
C. 4 D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?(
 =1.414)
=1.414) 
-
科目: 来源: 题型:
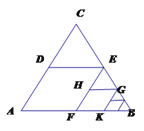
查看答案和解析>>【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.

(1)求A、B、C三点的坐标.
(2)求抛物线的对称轴及顶点坐标.
(3)抛物线上是否存在点F,使△ABF的面积为1?若存在,求F点的坐标;若不存在,请说明理由.
相关试题

