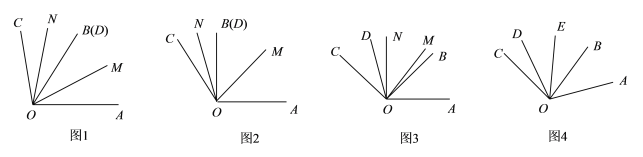
【题目】已知,如图1,∠AOB和∠COD共顶点O,OB和OD重合,OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β.
(1)如图2,若α=90°,β=30°,则∠MON=________;
(2)若将∠COD绕O逆时针旋转至图3的位置,求∠MON;(用α,β表示)
(3)如图4,若α=2β,∠COD绕O逆时针旋转,转速为3°/秒,∠AOB绕O同时逆时针旋转,转速为1°/秒(转到OC与OA共线时停止运动),且OE平分∠BOD,请判断∠COE与∠AOD的数量关系并说明理由.
参考答案:
【答案】(1)60°(2)![]() .(3)
.(3)![]() 为定值
为定值![]() .
.
【解析】
(1)利用角平分线的性质即可得出∠MON=![]() ∠AOD+
∠AOD+![]() ∠BOC,进而求出即可;
∠BOC,进而求出即可;
(2)设∠BOD=γ,而∠MOD=![]() =
=![]() ,∠NOB=
,∠NOB=![]() =
=![]() ,进而得出即可;
,进而得出即可;
(3)利用已知表示出∠COE和∠AOD,进而得出答案.
(1)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,α=90゜,β=30゜,
∴∠MON=![]() α+
α+![]() β=60°,
β=60°,
故答案为:60°;
(2)设∠BOD=γ,
∵∠MOD=![]() =
=![]() ,∠NOB=
,∠NOB=![]() =
=![]() ,
,
∴∠MON=∠MOD+∠NOB-∠DOB=![]() +
+![]() -γ=
-γ=![]() .
.
(3)![]() 为定值
为定值![]() .
.
设运动时间为t秒,则∠DOB=3t-t=2t,∠DOE=![]() ∠DOB=t,
∠DOB=t,
∴∠COE=β+t,∠AOD=α+2t,
又∵α=2β,
∴∠AOD=2β+2t=2(β+t),
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,当x>0时,y的值随x的值增大而减小的函数是( )
A.y=3x
B.y=x﹣1
C.y=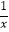
D.y=2x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=(k﹣3)x+k,给出下列结论:
①此函数是一次函数,
②无论k取什么值,函数图象必经过点(﹣1,3),
③若图象经过二、三、四象限,则k的取值范围是k<0,
④若函数图象与x轴的交点始终在正半轴可得k<3.其中正确的是( )
A. ①② B. ①③ C. ②③ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )

A.AB⊥AC
B.AB=AC
C.AB=BC
D.AC=BC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).
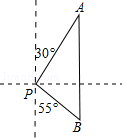
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,E为弦AC的延长线上一点,DE与⊙O相切于点D,且DE⊥AC,连结OD,若AB=10,AC=6,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
相关试题

