【题目】如图,AB是⊙O的直径,E为弦AC的延长线上一点,DE与⊙O相切于点D,且DE⊥AC,连结OD,若AB=10,AC=6,求DE的长. 
参考答案:
【答案】解:连结BC,如图,BC与OD相交于点F, ∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC⊥AE,
又∵DE⊥AC,
∴BC∥DE,
∵DE是⊙O的切线,
∴OD⊥DE,
∴OD⊥BC,
∴CF= ![]() BC,
BC,
∵BC⊥AE,DE⊥AC,DE⊥AC,
∴四边形CEDF是矩形.
∴DE=CF= ![]() BC,
BC,
在Rt△ACB中,∠ACB=90°,
∴BC= ![]() =8,
=8,
∴CF=4,
∴DE=4.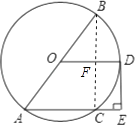
【解析】连结BC,如图,BC与OD相交于点F,利用圆周角定理得到BC⊥AE,则BC∥DE,再利用切线的性质得到OD⊥DE,接着利用垂径定理得到CF= ![]() BC,接下来判定四边形CEDF是矩形得到DE=CF=
BC,接下来判定四边形CEDF是矩形得到DE=CF= ![]() BC,然后利用勾股定理计算出BC,从而得到CF和DE的长.
BC,然后利用勾股定理计算出BC,从而得到CF和DE的长.
【考点精析】掌握勾股定理的概念和切线的性质定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )

A.AB⊥AC
B.AB=AC
C.AB=BC
D.AC=BC -
科目: 来源: 题型:
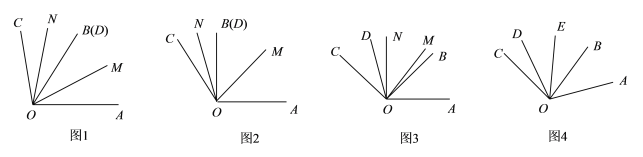
查看答案和解析>>【题目】已知,如图1,∠AOB和∠COD共顶点O,OB和OD重合,OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β.
(1)如图2,若α=90°,β=30°,则∠MON=________;
(2)若将∠COD绕O逆时针旋转至图3的位置,求∠MON;(用α,β表示)
(3)如图4,若α=2β,∠COD绕O逆时针旋转,转速为3°/秒,∠AOB绕O同时逆时针旋转,转速为1°/秒(转到OC与OA共线时停止运动),且OE平分∠BOD,请判断∠COE与∠AOD的数量关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).
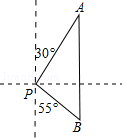
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两条线段,AB=2(单位长度),CD=1(单位长度)在数轴上运动,点A在数轴上表示的数是-12,点D在数轴上表示的数是15.
(1)点B在数轴上表示的数是________,点C在数轴上表示的数是________,线段BC的长=________;
(2)若线段AB以1个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.设运动时间为t秒,当BC=6(单位长度),求t的值;
(3)若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度/秒的速度也向左运动.设运动时间为t秒,当0<t<24时,M为AC中点,N为BD中点,则线段MN的长为________.

-
科目: 来源: 题型:
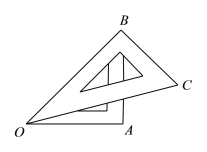
查看答案和解析>>【题目】如图,将一幅三角板摆放在一起.
(1)∠AOC的度数为________,射线OA 、OB、OC组成所有小于平角的和为________;
(2)反向延长射线OA 到D,OE为∠BOD的平分线,OF为∠COD的平分线,请按题意画出图形,并求出∠EOF的度数.
相关试题

