【题目】如图是一个量角器和一个含30°角的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OE.

(1)求证:DE∥CF;
(2)当OE=2时,若以O,B,F为顶点的三角形与△ABC相似,求OB的长;
(3)若OE=2,移动三角板ABC且使AB边始终与半圆O相切,直角顶点B在直径DE的延长线上移动,求出点B移动的最大距离.
参考答案:
【答案】(1)证明见解析(2)![]() 或4(3)3
或4(3)3
【解析】
试题分析:(1)先作辅助线,连接OF,证明四边形OBCF是平行四边形,得出DE∥CF;
(2)利用相似比求OB的长,
(3)由题意得到点B所在的两个极值位置,求出点B移动的最大距离.
(1)证明:连接OF,
∵AB切半圆O于点F,OF是半径,
∴∠OFB=90°,
∵∠ABC=90°,
∴∠OFB=∠ABC,
∴OF∥BC,
∵BC=OE,OE=OF,
∴BC=OF,
∴四边形OBCF是平行四边形,
∴DE∥CF;
(2)解:若△OBF∽△ACB,
∴![]() =
=![]() ,
,
∴OB=![]() ,
,
∵∠A=30°,∠ABC=90°,BC=OE=2,
∴AC=4,AB=2![]() .
.
又∵OF=OE=2,
∴OB=![]() =
=![]() ;
;
若△BOF∽△ACB,
∴![]() =
=![]() ,
,
∴OB=![]() ,
,
∴OB=![]() =4;
=4;
综上,OB=![]() 或4;
或4;
(3)解:画出移动过程中的两个极值图,
由图知:点B移动的最大距离是线段BE的长,
∵∠A=30°,∴∠ABO=30°,∴BO=4,∴BE=2,
∴点B移动的最大距离是线段BE的长为2.


-
科目: 来源: 题型:
查看答案和解析>>【题目】 (2016浙江台州第9题)小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )
A.1次 B.2次 C.3次 D.4次
-
科目: 来源: 题型:
查看答案和解析>>【题目】若式子2x+y的值是﹣4,则4x+2y+8的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式,成立的是( )
A. 2x2 +x2= 3x4 B. x+y=xy C. 2x2 –x2= x2 D. 6x-3x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,∠EBF=45°,△EDF的周长为8,则正方形ABCD的边长为( )
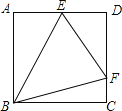
A.2 B.3 C.5 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线互相平分且相等的四边形是矩形
C. 对角线互相垂直平分的四边形是菱形
D. 对角线互相垂直且相等的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=3x2向上平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式为( )
A.y=3(x+2)2+3
B.y=3(x﹣2)2+3
C.y=3(x+2)2﹣3
D.y=3(x﹣2)2﹣3
相关试题

