【题目】在平面直角坐标系xOy中,图形W在坐标轴上的投影长度定义如下:
设点P![]() ,Q
,Q![]() 是图形W上的任意两点.若
是图形W上的任意两点.若![]() 的最大值为m,则图形W在x轴上的投影长度
的最大值为m,则图形W在x轴上的投影长度![]() =m;若
=m;若![]() 的最大值为n,则图形W在y轴上的投影长度
的最大值为n,则图形W在y轴上的投影长度![]() =n,如下图,图形W在x轴上的投影长度
=n,如下图,图形W在x轴上的投影长度![]() =
=![]() =2;在y轴上的投影长度
=2;在y轴上的投影长度![]() =
=![]() =4.
=4.
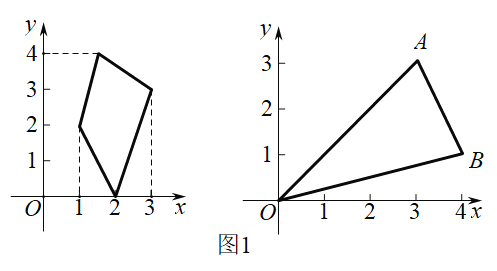
(1)已知点A(3,3),B(4,1).如图1所示,若图形W为△OAB,则![]() =___________
=___________ ![]() =___________
=___________
(2)已知点C(4,0),点D在直线y=-2x+6上,若图形W为△OCD.当=![]() 时,求点D的坐标.
时,求点D的坐标.
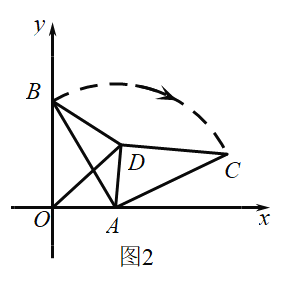
(3)如图2所示,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD,BD.若图形W为点O.A.C.D.B围成的多边形图象,且∠DOA=∠OBA,直接写出![]() 的值
的值
参考答案:
【答案】(1)![]() ;(2)点D的坐标为(1,4)或(6,-6),(3)
;(2)点D的坐标为(1,4)或(6,-6),(3)![]() 或
或![]()
【解析】
(1)确定出点A在y轴的投影的坐标、点B在x轴上投影的坐标,于是可求得问题的答案;
(2)过点P作PD⊥x轴,垂足为P.设D(x,-2x+6),则PD=|-2x+6|.PC=|4-x|,然后依据![]() ,列方程求解即可.
,列方程求解即可.
(3)分情况讨论,当D在第一象限时,由旋转的性质结合∠DOA=∠OBA,证明![]() 三点共线,过C作CF
三点共线,过C作CF![]() OB于F,过C作CG
OB于F,过C作CG![]() OA于G,设
OA于G,设![]() 利用勾股定理列出方程组即可得到答案.当D在第四象限时,过D作DF
利用勾股定理列出方程组即可得到答案.当D在第四象限时,过D作DF![]() OB于F,过D作DG
OB于F,过D作DG![]() OA于G,则四边形
OA于G,则四边形![]() 为矩形,设
为矩形,设![]() 建立方程组求解即可.
建立方程组求解即可.
解:(1)∵A(3,3),
∴点A在y轴上的正投影的坐标为(0,3).
∴△OAB在y轴上的投影长度![]() .
.
∵B(4,1),
∴点B在x轴上的正投影的坐标为(4,0).
∴△OAB在x轴上的投影长度![]() .
.
故答案为:4,3.
(2)如图1所示;过点P作PD⊥x轴,垂足为P.
0≤x≤3时,-2x+6=4, 解得x=1.
∴D(1,4).
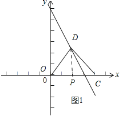
如图2所示:过点D作DP⊥x轴,垂足为P.
当3<x≤4时,
所以2x-6=4,
解得:x=5(舍去),
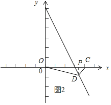
如图3所示,当点D在C点右侧,x>4时,
x=2x-6, 可得x=6 ,
点D坐标(6,-6),
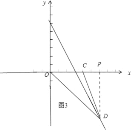
如图4所示:当 x<0时,-2x+6=4-x,
解得:x=2 舍去,
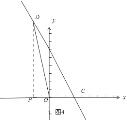
综上所述,点D的坐标为(1,4)或(6,-6).
(3)如图,当D在第一象限时,
![]() ∠DOA=∠OBA,
∠DOA=∠OBA,
![]()
![]()
![]()
由旋转可知:![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]()
![]() 三点共线,
三点共线,![]()
过C作CF![]() OB于F,过C作CG
OB于F,过C作CG![]() OA于G,
OA于G,
则四边形![]() 为矩形,
为矩形,
设![]()
![]()
![]()
![]()
由勾股定理得:
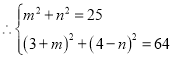
消去![]() 得:
得:![]()
![]()
![]() (舍去)
(舍去)
![]()
![]()
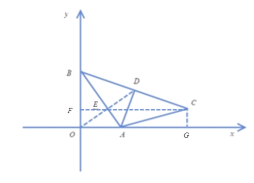
如下图,当点C旋转到![]() 轴的负半轴上,D在第四象限时,
轴的负半轴上,D在第四象限时,
![]()
![]()
同理可得:![]() 是
是![]() 的垂直平分线,
的垂直平分线,
过D作DF![]() OB于F,过D作DG
OB于F,过D作DG![]() OA于G,
OA于G,
则四边形![]() 为矩形,
为矩形,
设![]()
同理可得:
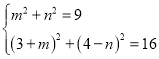
消去![]() 得:
得:![]()
![]()
![]() (舍去)
(舍去)
![]()
此时:![]()
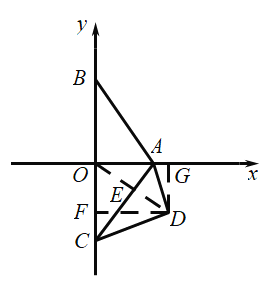
综上:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
新定义:任意两数a.b,按规定
 得到一个新数c,称所得新数c为数a.b的“快乐返校学习数”.
得到一个新数c,称所得新数c为数a.b的“快乐返校学习数”.(1)若a=1,b=2,求a,b的“快乐返校学习数”c.
(2)若
 ,b=
,b= ,且
,且 (0<m<1),求a,b的“快乐返校学习数”c.
(0<m<1),求a,b的“快乐返校学习数”c.(3)若a=2n+1,b=n-1,且a,b的“快乐返校学习数”c为正整数,求整数n的值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若取前3格子中的任意两个数记作
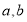 ,且
,且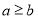 ,那么所有的
,那么所有的 的和可以通过计算
的和可以通过计算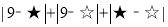 得到,其结果为_____,若
得到,其结果为_____,若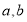 为前
为前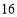 格子中的任意两个数,且
格子中的任意两个数,且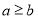 ,则所有的
,则所有的 的和为_____.
的和为_____.9
★
☆
x
﹣6
2
……
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为__________度,该班共有学生__________人,训练后篮球定时定点投篮平均每个人的进球数是__________.
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
-
科目: 来源: 题型:
查看答案和解析>>【题目】请观察下列算式,找出规律并填空
 =1-
=1- ,
,  =
= -
- ,
,  =
= -
- ,
,  =
= -
-
则第10个算式是 _____________=_____________
第n个算式是 ___________=_____________
根据以上规律解答以下三题:(1)

(2)若有理数a、b满足|a-1|+
 =0 ,试求:
=0 ,试求: +
+ +
+ + …+
+ …+ 的值.
的值.
相关试题

