【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
参考答案:
【答案】C
【解析】分析:过F作AB、CD的平行线FG,由于F是AD的中点,那么G是BC的中点,即Rt△BCE斜边上的中点,由此可得BC=2EG=2FG,即△GEF、△BEG都是等腰三角形,因此求∠B的度数,只需求得∠BEG的度数即可;易知四边形ABGF是平行四边形,得∠EFG=∠AEF,由此可求得∠FEG的度数,即可得到∠AEG的度数,根据邻补角的定义可得∠BEG的值,由此得解.
详解:过F作FG∥AB∥CD,交BC于G;
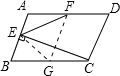
则四边形ABGF是平行四边形,所以AF=BG,
即G是BC的中点;
连接EG,在Rt△BEC中,EG是斜边上的中线,
则BG=GE=FG=![]() BC;
BC;
∵AE∥FG,
∴∠EFG=∠AEF=∠FEG=54°,
∴∠AEG=∠AEF+∠FEG=108°,
∴∠B=∠BEG=180°-108°=72°.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,图形W在坐标轴上的投影长度定义如下:
设点P
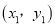 ,Q
,Q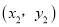 是图形W上的任意两点.若
是图形W上的任意两点.若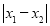 的最大值为m,则图形W在x轴上的投影长度
的最大值为m,则图形W在x轴上的投影长度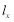 =m;若
=m;若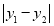 的最大值为n,则图形W在y轴上的投影长度
的最大值为n,则图形W在y轴上的投影长度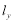 =n,如下图,图形W在x轴上的投影长度
=n,如下图,图形W在x轴上的投影长度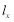 =
=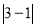 =2;在y轴上的投影长度
=2;在y轴上的投影长度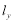 =
=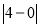 =4.
=4.(1)已知点A(3,3),B(4,1).如图1所示,若图形W为△OAB,则
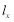 =___________
=___________  =___________
=___________(2)已知点C(4,0),点D在直线y=-2x+6上,若图形W为△OCD.当=
 时,求点D的坐标.
时,求点D的坐标.(3)如图2所示,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD,BD.若图形W为点O.A.C.D.B围成的多边形图象,且∠DOA=∠OBA,直接写出
 的值
的值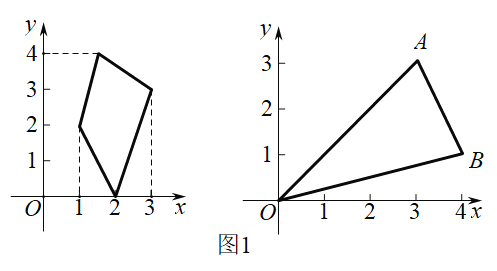
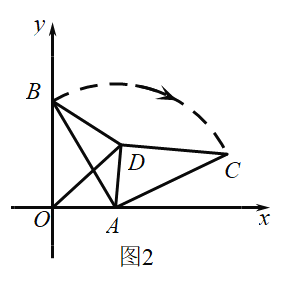
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为__________度,该班共有学生__________人,训练后篮球定时定点投篮平均每个人的进球数是__________.
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请观察下列算式,找出规律并填空
 =1-
=1- ,
,  =
= -
- ,
,  =
= -
- ,
,  =
= -
-
则第10个算式是 _____________=_____________
第n个算式是 ___________=_____________
根据以上规律解答以下三题:(1)

(2)若有理数a、b满足|a-1|+
 =0 ,试求:
=0 ,试求: +
+ +
+ + …+
+ …+ 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的八年级知识竞赛中,每班参加比赛的人数相同,成绩分为
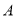 、
、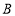 、
、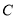 、
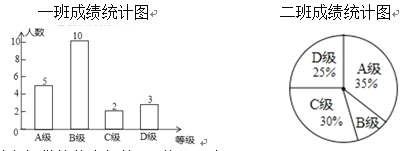
、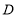 四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将一班和二班的成绩整理并绘制成如下的统计图:
四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:
(1)求一班参赛选手的平均成绩;
(2)此次竞赛中,二班成绩在
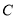 级以上(包括
级以上(包括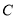 级)的人数有几人?
级)的人数有几人?(3)求二班参赛选手成绩的中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进
 、
、 两种新型节能台灯共
两种新型节能台灯共 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:
(
 )若商场预计进货款为
)若商场预计进货款为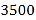 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?(
 )若商场规定
)若商场规定 型台灯的进货数量不超过
型台灯的进货数量不超过 型台灯数量的
型台灯数量的 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
相关试题

