【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M. 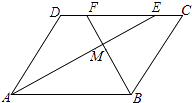
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
参考答案:
【答案】
(1)解:方法一:如图①,
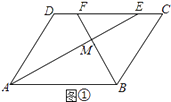
∵在ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
方法二:如图②,延长BC、AE相交于点P,
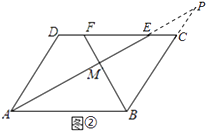
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴AB=BP.
∵BF平分∠ABP,
∴AP⊥BF,
即AE⊥BF
(2)解:方法一:线段DF与CE是相等关系,即DF=CE,
∵在ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.
∴∠DEA=∠DAE.
∴DE=AD.
同理可得,CF=BC.
又∵在ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.
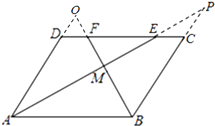
方法二:如图,延长BC、AE设交于点P,延长AD、BF相交于点O,
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴BP=AB.
同理可得,AO=AB.
∴AO=BP.
∵在ABCD中,AD=BC,
∴OD=PC.
又∵在ABCD中,DC∥AB,
∴△ODF∽△OAB,△PCE∽△PBA.
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
∴DF=CE.
【解析】(1)因为AE,BF分别是∠DAB,∠ABC的角平分线,那么就有∠MAB= ![]() ∠DAB,∠MBA=
∠DAB,∠MBA= ![]() ∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
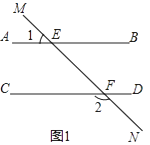
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,PF∥GH,求证:GH⊥EG;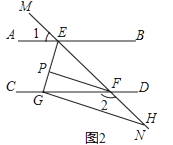
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.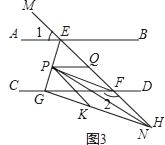
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1,60)
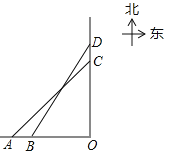
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B.
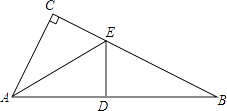
(1)求∠B的度数.
(2)如果AC=3cm,求AB的长度.
(3)猜想:ED与AB的位置关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
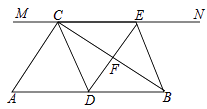
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截去正方体的一个角,则截面不可能是( )
A. 等腰直角三角形 B. 等腰三角形
C. 锐角三角形 D. 等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
(1)用α和β的三角函数表示CE;
(2)当α=30°、β=60°时,求EF(结果精确到1m).
(参考数据:
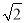 ≈1.414,
≈1.414,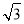 ≈1.732)
≈1.732)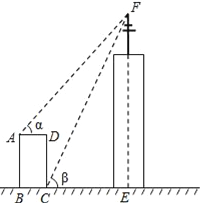
相关试题

