【题目】如图是某工厂货物传送带的平面示意图,为提高传送过程的安全性,工厂计划改造传动带与地面的夹角,使其AB的坡角由原来的43°改为30°.已知原传送带AB长为5米.求新旧货物传送带着地点B、C之间相距多远?(结果保留整数,参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
参考答案:
【答案】解:过点A作AD垂直于CB的延长线于点D.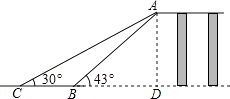
在Rt△ADB中,AB=5米,∠ABD=43°,
∵sin∠ABD= ![]() ,cos∠ABD=
,cos∠ABD= ![]() ,
,
∴AD=ABsin∠ABD=5×sin43°≈3.41米,
BD=ABcos∠ABD=5×cos43°≈3.66米.
在Rt△ADC中,
∵sin∠ACD= ![]() ,
,
AC= ![]() =6.82米,
=6.82米,
在Rt△ACD中,AC=6.82,∠ACD=30°,
∵cos∠ACD= ![]() ,
,
CD=ACcos∠ACD≈6.82×cos30°≈5.91米.
∴BC=CD﹣BD≈2米.
答:新旧货物传送带着地点B、C之间大约相距2米.
【解析】过A作BC的垂线AD.在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.再通过解直角三角形,可求出BD、CD的长,进而可求出BC的长.
【考点精析】利用关于坡度坡角问题对题目进行判断即可得到答案,需要熟知坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号)
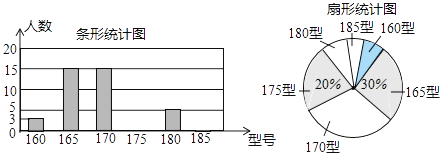
根据以上信息,解答下列问题:
(1)该班共有名学生;
(2)在扇形统计图中,185型校服所对应的扇形圆心角的大小为;
(3)该班学生所穿校服型号的众数为 , 中位数为;
(4)如果该校预计招收新生600名,根据样本数据,估计新生穿170型校服的学生大约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅计划购买12张餐桌和一批椅子(不少于12把),现从甲、乙两商场了解到同一型号的餐桌报价都为每张200元,餐椅报价都为每把50元.甲商场规定:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八五折销售,那么,什么情况下到甲商场购买更优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
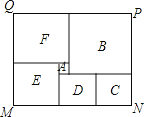
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线y=
 经过点B(3
经过点B(3 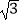 ,1),点A是双曲线第三象限上的动点,过B作BC⊥y轴,垂足为C,连接AC.
,1),点A是双曲线第三象限上的动点,过B作BC⊥y轴,垂足为C,连接AC. 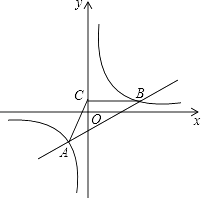
(1)求k的值;
(2)若△ABC的面积为6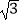 ,求直线AB的解析式;
,求直线AB的解析式;
(3)在(2)的条件下,写出反比例函数值大于一次函数值时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=
 ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店购买一批时令水果,在20天内销售完毕,店主将本次此销售数据绘制成函数图象,如图①,日销售量y(千克)与销售时间x(天)之间的函数关系;如图②,销售单价p(元/千克)与销售时间x(天)之间的函数关系式.

(1)求y关于x和p关于x的函数关系式;
(2)若日销售量不低于36千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售金额最高是第几天?
相关试题

