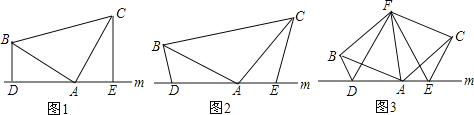
【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可).
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问第(1)题中DE、BD、CE之间的关系是否仍然成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断线段DF、EF的数量关系,并说明理由.
参考答案:
【答案】(1) DE=BD+CE;(2)DE=BD+CE的关系仍然成立.理由见解析;(3) DF=EF.理由见解析.
【解析】
(1)利用已知得出∠CAE=∠ABD,进而利用AAS得出则△ABD≌△CAE,即可得出DE=BD+CE;
(2)根据∠BDA=∠AEC=∠BAC=α,得出∠CAE=∠ABD,在△ADB和△CEA中,根据AAS证出△ADB≌△CEA,从而得出AE=BD,AD=CE,即可证出DE=BD+CE;
(3)与前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,利用“SAS”可判断△DBF≌△EAF,所以DF=EF.
解:(1)DE、BD、CE三条线段之间的数量关系是DE=BD+CE.理由如下: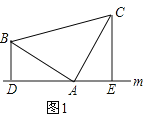
如图1,∵BD⊥m,CE⊥m,
∴∠BDA=∠AEC=90°
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
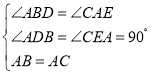
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD;
(2)如图2,

∵∠BDA=∠AEC=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中
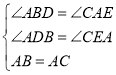
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴BD+CE=AE+AD=DE;
(3)DF=EF.理由如下:
由(2)知,△ADB≌△CAE,
BD=EA,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,BF=AF
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
在△DBF和△EAF中,
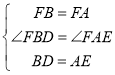
∴△DBF≌△EAF(SAS),
∴DF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在△ABC 中,AB=AC,D、E 是 BC 上异于 B、C 的任意两点,连接 AD 和 AE,且AD=AE.
(1)图中有几组全等三角形?请分别写出来;
(2)选择其中的一组证明两三角形全等.

-
科目: 来源: 题型:
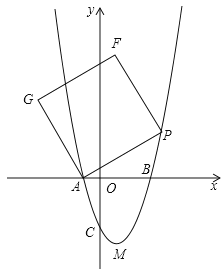
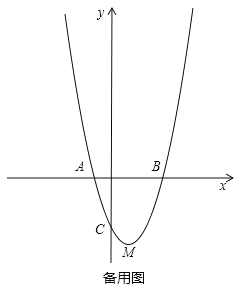
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,把抛物线
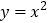 先向右平移1个单位,再向下平移4个单位,得到抛物线
先向右平移1个单位,再向下平移4个单位,得到抛物线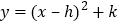 ,所得抛物线与x轴交于A、B两点
,所得抛物线与x轴交于A、B两点 点A在点B的左边
点A在点B的左边 ,与y轴交于点C,顶点为M;
,与y轴交于点C,顶点为M; 写出h、k的值以及点A、B的坐标;
写出h、k的值以及点A、B的坐标; 判断三角形BCM的形状,并计算其面积;
判断三角形BCM的形状,并计算其面积; 点P是抛物线上一动点,在y轴上找点
点P是抛物线上一动点,在y轴上找点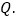 使点A,B,P,Q组成的四边形是平行四边形,直接写出对应的点P的坐标
使点A,B,P,Q组成的四边形是平行四边形,直接写出对应的点P的坐标 不用写过程
不用写过程
 点P是抛物线上一动点,连接AP,以AP为一边作正方形APFG,随着点P的运动,正方形的大小、位置也随之改变
点P是抛物线上一动点,连接AP,以AP为一边作正方形APFG,随着点P的运动,正方形的大小、位置也随之改变 当顶点F或G恰好落在y轴上时,请直接写出对应的点P的坐标
当顶点F或G恰好落在y轴上时,请直接写出对应的点P的坐标 不写过程
不写过程

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系
 中,已知点
中,已知点 的坐标
的坐标 ,过
,过 点作
点作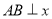 轴,垂足为点
轴,垂足为点 ,过点
,过点 作直线
作直线 轴,点
轴,点 从点
从点 出发在
出发在 轴上沿着轴的正方向运动.
轴上沿着轴的正方向运动.
(1)当点
 运动到点
运动到点 处,过点
处,过点 作
作 的垂线交直线
的垂线交直线 于点
于点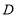 ,证明
,证明 ,并求此时点
,并求此时点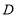 的坐标;
的坐标;(2)点
 是直线
是直线 上的动点,问是否存在点
上的动点,问是否存在点 ,使得以
,使得以 为顶点的三角形和
为顶点的三角形和 全等,若存在求点
全等,若存在求点 的坐标以及此时对应的点
的坐标以及此时对应的点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:任意两个数a 、b ,按规则c = a +b-ab 扩充得到一个新数c ,称所得的新数c 为“如意数”.
(1)若a =2, b =-3,直接写出a 、b 的“如意数” c ;
(2)若a =2, b = x2 +1,求a 、b 的“如意数” c ,并比较b 与c 的大小;
(3)已知a=x2-1,且a 、b 的“如意数” c = x3 +3x2-1,则b = (用含 x 的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明学习了《有理数》后,对运算非常感兴趣,于是定义了一种新运算“△”规则如下:对于两个有理数m , n , m △ n =
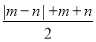 .
.(1)计算:1△(-2)= ;
(2)判断这种新运算是否具有交换律,并说明理由;
(3)若a
 =| x-1| , a
=| x-1| , a =| x-2|,求a
=| x-2|,求a △ a
△ a  (用含 x 的式子表示)
(用含 x 的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将函数y=
 (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A.
 B.
B. 
C.
 D.
D. 
相关试题

