搜索
【题目】计算：
(1)(0.2x－0.3)(0.2x＋0.3)；
(2)(2a3b2－4a4b3＋6a5b4)÷(－2a3b2)．
参考答案：
【答案】（1）0.04x2－0.09；（2）－1＋2ab－3a2b2
【解析】
（1）利用平方差公式进行计算即可得出答案；
（2）利用多项式除以单项式的计算法则进行计算即可得出答案.
解：(1)原式＝(0.2x)2－0.32＝0.04x2－0.09；
(2)原式＝2a3b2÷(－2a3b2)－4a4b3÷(－2a3b2)＋6a5b4÷(－2a3b2)＝－1＋2ab－3a2b2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=2x+4的图象与y轴交点的坐标是（ ）
A.（0，﹣4）
B.（0，4）
C.（2，0）
D.（﹣2，0） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．
（1）求证：AE=BF；
（2）连接GB，EF，求证：GB∥EF；
（3）若AE=1，EB=2，求DG的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：a2+3a= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：(3x＋2y)2－(3x－2y)2＋2(x＋y)(x－y)－2x(x＋4y)，其中x＝1，y＝－1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=5cm，点D在边BC上，且CD=3cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以1cm/s的速度沿AC向终点运动；点Q以1.25cm/s的速度沿BC向终点C运动，过点P作PE∥BC交AD于点E，连接EQ，设动点运动时间为ts（0＜t＜4）．
（1）连接DP，当t＞1时，四边形EQDP能够成为平行四边形吗？请说明理由；
（2）连接PQ，在运动过程中，不论t取何值，总有PQ与AB平行．为什么？
（3）当t为何值时，△EDQ为直角三角形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
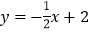分别交y轴、x轴于A、B两点，抛物线y=﹣x2+bx+c过A、B两点．（1）求这个抛物线的解析式；
（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？
（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．
相关试题
