Question

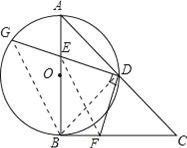
【题目】如图，在Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．

（1）求证：AE=BF；

（2）连接GB，EF，求证：GB∥EF；

（3）若AE=1，EB=2，求DG的长．

Answer 1

【答案】（1）（2）见解析 （3）．

【解析】（1）连接BD，由三角形ABC为等腰直角三角形，求出∠A与∠C的度数，根据AB为圆的直径，利用圆周角定理得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD=AC，进而确定出∠A=∠FBD，再利用同角的余角相等得到一对角相等，利用ASA得到三角形AED与三角形BFD全等，利用全等三角形对应边相等即可得证；

（2）连接EF，BG，由三角形AED与三角形BFD全等，得到ED=FD，进而得到三角形DEF为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行即可得证；

（3）由全等三角形对应边相等得到AE=BF=1，在直角三角形BEF中，利用勾股定理求出EF的长，利用锐角三角形函数定义求出DE的长，利用两对角相等的三角形相似得到三角形AED与三角形GEB相似，由相似得比例，求出GE的长，由GE+ED求出GD的长即可．

（1）证明：连接BD，

在Rt△ABC中，∠ABC=90°，AB=BC，

∴∠A=∠C=45°，

∵AB为圆O的直径，

∴∠ADB=90°，即BD⊥AC，

∴AD=DC=BD=AC，∠CBD=∠C=45°，

∴∠A=∠FBD，

∵DF⊥DG，

∴∠FDG=90°，

∴∠FDB+∠BDG=90°，

∵∠EDA+∠BDG=90°，

∴∠EDA=∠FDB，

在△AED和△BFD中，

∠A=∠FBD，AD=BD，∠EDA=∠FDB，

∴△AED≌△BFD（ASA），

∴AE=BF；

（2）证明：连接EF，BG，

∵△AED≌△BFD，

∴DE=DF，

∵∠EDF=90°，

∴△EDF是等腰直角三角形，

∴∠DEF=45°，

∵∠G=∠A=45°，

∴∠G=∠DEF，

∴GB∥EF；

（3）∵AE=BF，AE=1，

∴BF=1，

在Rt△EBF中，∠EBF=90°，

∴根据勾股定理得：EF2=EB2+BF2，

∵EB=2，BF=1，

∴EF=，

∵△DEF为等腰直角三角形，∠EDF=90°，

∴cos∠DEF=，

∵EF=，

∴DE=×，

∵∠G=∠A，∠GEB=∠AED，

∴△GEB∽△AED，

∴，即GEED=AEEB，

∴GE=2，即GE=，

则GD=GE+ED=．