搜索
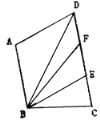
【题目】如图,AB∥CD,点E为CD上一点,连接BE,AD∥BE,连接BD,BD平分∠ABE,BF平分∠ABC交CD于点F, ∠ABC=100°，∠DBF=14°,∠ADC的度数为_______°.
参考答案：
【答案】72
【解析】
根据∠ABC=100°，BF平分∠ABC得到∠ABF=50°，根据∠DBF=14°得到∠ABD=36°，又BD平分∠ABE，故∠ABE=2∠ABD=72°，再根据AD∥BE，AB∥CD即可求解∠ADC.
∵∠ABC=100°，BF平分∠ABC
∴∠ABF=
∠ABC=50°，
∵∠DBF=14°
∴∠ABD=∠ABF -∠DBF =36°，
又BD平分∠ABE，
∴∠ABE=2∠ABD=72°，
∵AD∥BE，∴∠BAD=180°-∠ABE=108°，
∵AB∥CD
∴∠ADC=180°-∠BAD =72°
故填：72.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形ABCD中，E、F分别为BC、CD边上的两个动点，∠EAF＝45°，下列几个结论中：①EF＝BE＋DF；②MN2＝BM2＋DN2；③FA平分∠DFE；④连接MF，则△AMF为等腰直角三角形；⑤∠AMN＝∠AFE． 其中一定成立的结论有（ ）
A.2个B.3个C.4个D.5个
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知直线y
x＋3与x轴、y轴分别交于A、B两点，点C在线段OB上，把△ABC沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标是_____． -
科目： 来源： 题型：
查看答案和解析>>【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程mx2－(m+2)x＋2=0（m≠0）
(1)求证：方程一定有两个实数根；
(2)若此方程的两根为不相等的整数，求整数m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店经销一种健身球，已知这种健身球的成本价为每个20元，市场调查发现，该种健身球每天的销售量y（个）与销售单价x（元）有如下关系：y=﹣20x+80（20≤x≤40），设这种健身球每天的销售利润为w元．
（1）求w与x之间的函数关系式；
（2）该种健身球销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
（3）如果物价部门规定这种健身球的销售单价不高于28元，该商店销售这种健身球每天要获得150元的销售利润，销售单价应定为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），抛物线
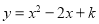与x轴交于A、B两点，与y轴交于点C（0，
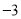）．［图（2）为解答备用图］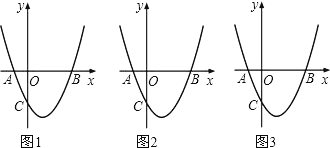
（1）
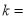__________，点A的坐标为___________，点B的坐标为__________；（2）设抛物线
的顶点为M，求四边形ABMC的面积；（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．
相关试题
