【题目】如图(1),抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).[图(2)为解答备用图]
).[图(2)为解答备用图]
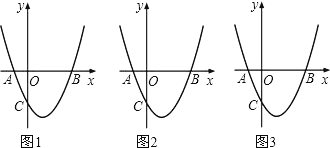
(1)![]() __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) k=-3,A(-1,0),B(3,0);(2)9;(3) ![]() .
.
【解析】
试题分析:(1)将C点坐标代入抛物线的解析式中,即可求出k的值;令抛物线的解析式中y=0,即可求出A、B的坐标;
(2)将抛物线的解析式化为顶点式,即可求出M点的坐标;由于四边形ACMB不规则,可连接OM,将四边形ACMB的面积转化为△ACO、△MOC以及△MOB的面积和;
(3)当D点位于第三象限时四边形ABCD的最大面积显然要小于当D位于第四象限时四边形ABDC的最大面积,因此本题直接考虑点D为与第四象限时的情况即可;设出点D的横坐标,根据抛物线的解析式即可得到其纵坐标;可参照(2)题的方法求解,连接OD,分别表示出△ACO、△DOC以及△DOB的面积,它们的面积和即为四边形ABDC的面积,由此可得到关于四边形ABDC的面积与D点横坐标的函数关系式,根据函数的性质即可求出四边形ABDC的最大面积及对应的D点坐标.
试题解析:(1)由于点C在抛物线的图象上,则有:k=-3;
∴y=x2-2x-3;
令y=0,则x2-2x-3=0,
解得x=-1,x=3,
∴A(-1,0),B(3,0);
(2)抛物线的顶点为M(1,-4),连接OM;
则△AOC的面积=![]() AOOC=
AOOC=![]() ×1×3=
×1×3=![]() ,
,
△MOC的面积=![]() OC|xM|=
OC|xM|=![]() ×3×1=
×3×1=![]() ,
,
△MOB的面积=![]() OB|yM|=
OB|yM|=![]() ×3×4=6;
×3×4=6;
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9;
(3)设D(m,m2-2m-3),连接OD;
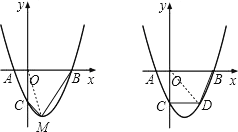
则0<m<3,m2-2m-3<0;
且△AOC的面积=![]() ,△DOC的面积=
,△DOC的面积=![]() m,△DOB的面积=-
m,△DOB的面积=-![]() (m2-2m-3);
(m2-2m-3);
∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
=-![]() m2+
m2+![]() m+6=-
m+6=-![]() (m-
(m-![]() )2+
)2+![]() ;
;
∴存在点D(![]() ,-
,-![]() ),使四边形ABDC的面积最大,且最大值为
),使四边形ABDC的面积最大,且最大值为![]() .
.
-
科目: 来源: 题型:
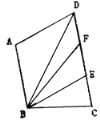
查看答案和解析>>【题目】如图,AB∥CD,点E为CD上一点,连接BE,AD∥BE,连接BD,BD平分∠ABE,BF平分∠ABC交CD于点F, ∠ABC=100°,∠DBF=14°,∠ADC的度数为_______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2-(m+2)x+2=0(m≠0)
(1)求证:方程一定有两个实数根;
(2)若此方程的两根为不相等的整数,求整数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
-
科目: 来源: 题型:
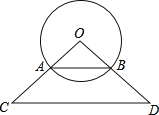
查看答案和解析>>【题目】已知⊙O的半径为12cm,弦AB=12
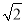 cm.
cm.(1)求圆心O到弦AB的距离.
(2)若弦AB恰好是△OCD的中位线,以CD中点E为圆点,R为半径作⊙E,当⊙O和⊙E相切时,求R的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图中的折线ABC表示某汽车的耗油量y(L/km)与速度x(km/h)之间的函数关系(30≤x≤120).已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
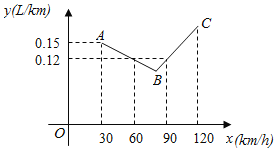
(1)当30≤x≤120时,求y与x之间的函数表达式;
(2)该汽车的速度是多少时,耗油量最低?最低是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
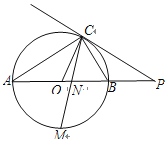
(1)求证:PC是⊙O的切线;
(2)求证:BC=
 AB;
AB;(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN
 MC的值.
MC的值.
相关试题

