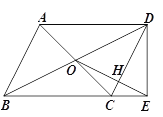
【题目】如图,□ABCD的对角线相交于点O,将线段OD绕点O旋转,使点D的对应点落在BC延长线上的点E处,OE交CD于H,连接DE.
(1)求证:DE⊥BC;
(2)若OE⊥CD,求证:2CE·OE=CD·DE;
(3)若OE⊥CD,BC=3,CE=1,求线段AC的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】(1)由平行四边形的性质得到BO=![]() BD,根据平行四边形的判定即可得到结论;(2)根据等角的余角相等,得到∠CEO=∠CDE,推出△CDE∽△DBE,即可得到结论;
BD,根据平行四边形的判定即可得到结论;(2)根据等角的余角相等,得到∠CEO=∠CDE,推出△CDE∽△DBE,即可得到结论;
(3)由第二问所得的相似求出DE,再由勾股定理求出AC即可.
解:(1)证明:由旋转可知OE=OD,∴∠ODE=∠OED
∵四边形ABCD是平行四边形,∴OB=OD,OA=OC
∴OB=OE,∴∠OEB=∠OBE
∵∠BDE+∠DBE+∠BED=180°,∴∠ODE+∠OED+∠OEB+∠OBE=180°
∴∠OED+∠OEB=90°,即∠DEB=90°,∴BC⊥CD
(2)∵OE⊥CD,∴∠CHE=90°,∴∠CDE+∠OED=90°
∵∠OED+∠OEB=90°,∴∠CDE=∠OEB
∵∠OEB=∠OBE,∴∠CDE=∠OBE
∵∠CDE=∠OBE,∠CED=∠DEB,∴△CDE∽△DBE
∴![]() ,即CE·BD=CD·DE
,即CE·BD=CD·DE
∵OE=OD,OB=OD,BD=OB+OD,∴BD=2OE
∴2CE·OE=CD·DE
(3)∵BC=3,CE=1,∴BE=4
由(2)知,△CDE∽△DBE
∴![]() ,即DE2=CE·BE=4,∴DE=2
,即DE2=CE·BE=4,∴DE=2
过点O作OF⊥BE,垂足为F
∵OB=OE,∴BF=EF=![]() BE=2,∴CF=EF-CE=1
BE=2,∴CF=EF-CE=1
∵OB=OD,BE=EF,∴OF=![]() DE=1
DE=1
在Rt△OCF中, ![]()
∴AC=2OC=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个多项式化成几个______,叫做因式分解. 因式分解和整式乘法具有_____的关系.
-
科目: 来源: 题型:
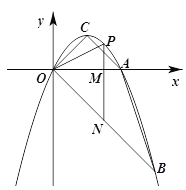
查看答案和解析>>【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0.那么我们称这个方程为“凤凰”方程,已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论:①a=c,②a=b,③b=c,④a=b=c,正确的是_____(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣3,4)关于原点对称的点的坐标为( )
A.(﹣3,﹣4)B.(3,﹣4)C.(﹣4,﹣3)D.(﹣3,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售部有营销人员20人,销售部为了制定某种商品的月销售额,统计了这20人的销售额如下:
销售额(万元)
13
14
15
16
17
18
19
20
频数(个)
1
1
5
4
3
2
3
1
(1)求这20位营销人员月销售额的平均数、中位数;
(2)假设你是销售部负责人,你认为把每位营销人员的月销售额定为多少合适?请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )
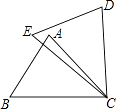
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D
D.BC=EC,∠A=∠D
相关试题

