【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )
A.
B.
C.
D.
参考答案:
【答案】B
【解析】解:当0≤t≤2时,如图,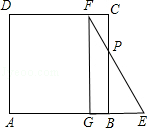
BG=t,BE=2﹣t,
∵PB∥GF,
∴△EBP∽△EGF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴PB=4﹣2t,
∴S= ![]() (PB+FG)GB=
(PB+FG)GB= ![]() (4﹣2t+4)t=﹣t2+4t;
(4﹣2t+4)t=﹣t2+4t;
当2<t≤4时,S= ![]() FGGE=4;
FGGE=4;
当4<t≤6时,如图,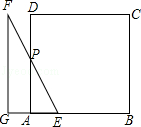
GA=t﹣4,AE=6﹣t,
∵PA∥GF,
∴△EAP∽△EGF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴PA=2(6﹣t),
∴S= ![]() PAAE=
PAAE= ![]() ×2×(6﹣t)(6﹣t)
×2×(6﹣t)(6﹣t)
=(t﹣6)2 ,
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选:B.
分类讨论:当0≤t≤2时,BG=t,BE=2﹣t,运用△EBP∽△EGF的相似比可表示PB=4﹣2t,S为梯形PBGF的面积,则S= ![]() (4﹣2t+4)t=﹣t2+4t,其图象为开口向下的抛物线的一部分;
(4﹣2t+4)t=﹣t2+4t,其图象为开口向下的抛物线的一部分;
当2<t≤4时,S= ![]() FGGE=4,其图象为平行于x轴的一条线段;
FGGE=4,其图象为平行于x轴的一条线段;
当4<t≤6时,GA=t﹣4,AE=6﹣t,运用△EAP∽△EGF的相似比可得到PA=2(6﹣t),所以S为三角形PAE的面积,则S=(t﹣6)2 , 其图象为开口向上的抛物线的一部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学本学年每个单元的测验成绩如下(单位:分):
甲:98,100,100,90,96,91,89,99,100,100,93
乙:98,99,96,94,95,92,92,98,96,99,97
(1)、他们的平均成绩分别是多少?
(2)、甲、乙的11次单元测验成绩的标准差分别是多少?
(3)、这两位同学的成绩各有什么特点?
(4)、现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围是( )
A.k>﹣
B.k≥﹣ 且k≠0
且k≠0
C.k≥﹣
D.k>﹣ 且k≠0
且k≠0 -
科目: 来源: 题型:
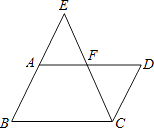
查看答案和解析>>【题目】如图,ABCD,E是BA延长线上一点,AB=AE,连接CE交AD于点F,若CF平分∠BCD,AB=3,则BC的长为 .
-
科目: 来源: 题型:
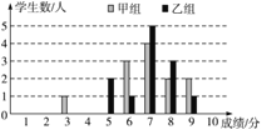
查看答案和解析>>【题目】(8分)一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
平均分
方差
中位数
合格率
优秀率
甲组
6.9
2.4
91.7%
16.7%
乙组
1.3
83.3%
8.3%
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=
 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
相关试题

