搜索
【题目】如图，ABCD，E是BA延长线上一点，AB=AE，连接CE交AD于点F，若CF平分∠BCD，AB=3，则BC的长为 ．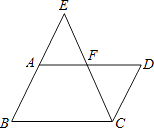 
参考答案：
【答案】6
【解析】解：∵CF平分∠BCD， 
∴∠BCE=∠DCF，
∵AD∥BC，
∴∠BCE=∠DFC，
∴∠BCE=∠EFA，
∵BE∥CD，
∴∠E=∠DCF，
∴∠E=∠BCE，
∵AD∥BC，
∴∠BCE=∠EFA，
∴∠E=∠EFA，
∴AE=AF=AB=3，
∵AB=AE，AF∥BC，
∴△AEF∽△BEC，
∴ 
= 
= 
= 
，
∴BC=2AF=6．
所以答案是：6．
【考点精析】掌握平行四边形的性质是解答本题的根本，需要知道平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两位同学本学年每个单元的测验成绩如下（单位：分）：
甲：98，100，100，90，96，91，89，99，100，100，93
乙：98，99，96，94，95，92，92，98，96，99，97
(1)、他们的平均成绩分别是多少？
(2)、甲、乙的11次单元测验成绩的标准差分别是多少？
(3)、这两位同学的成绩各有什么特点？
(4)、现要从中选出一人参加“希望杯”竞赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这项竞赛，为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=kx2﹣7x﹣7的图象和x轴有交点，则k的取值范围是（ ）
A.k＞﹣
B.k≥﹣ 且k≠0
C.k≥﹣
D.k＞﹣ 且k≠0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合．正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动，当点A和点E重合时正方形停止运动．设正方形的运动时间为t秒，正方形ABCD与Rt△GEF重叠部分面积为S，则S关于t的函数图象为（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
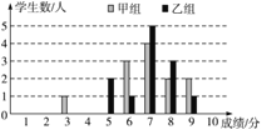
查看答案和解析>>【题目】（8分）一次学科测验，学生得分均为整数，满分10分，成绩达到6分以上（包括6分）为合格，成绩达到9分为优秀．这次测验中甲、乙两组学生成绩分布的条形统计图如图．
（1）请补充完成下面的成绩统计分析表：
平均分
方差
中位数
合格率
优秀率
甲组
6．9
2．4
91．7%
16．7%
乙组
1．3
83．3%
8．3%
（2）甲组学生说他们的合格率、优秀率均高于乙组，所以他们的成绩好于乙组．但乙组学生不同意甲组学生的说法，认为他们组的成绩要高于甲组．请你给出三条支持乙组学生观点的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（ ）
A. OE=
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE -
科目： 来源： 题型：
查看答案和解析>>【题目】典典同学学完统计知识后，随机调查了她家所在辖区若干名居民的年龄，将调查数据绘制成如下扇形和条形统计图：
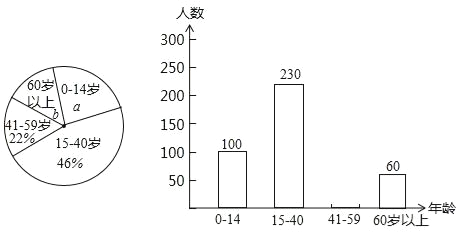
请根据以上不完整的统计图提供的信息，解答下列问题：
（1）扇形统计图中a= ，b= ；并补全条形统计图；
（2）若该辖区共有居民3500人，请估计年龄在0～14岁的居民的人数．
（3）一天，典典知道了辖区内60岁以上的部分老人参加了市级门球比赛，比赛的老人们分成甲、乙两组，典典很想知道甲乙两组的比赛结果，王大爷告诉说，甲组与乙组的得分和为110，甲组得分不低于乙组得分的1.5倍，甲组得分最少为多少？
相关试题
