【题目】在△ABC中,BC=AC,∠C=90°,直角顶点C在x轴上,一锐角顶点B在y轴上.
(1)如图①若AD于垂直x轴,垂足为点D.点C坐标是(﹣1,0),点A的坐标是(﹣3,1),求点B的坐标.
(2)如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,请猜想BD与AE有怎样的数量关系,并证明你的猜想.
(3)如图③,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,请猜想OC,AF,OB之间有怎样的关系(直接写出结论,不需要证明)

参考答案:
【答案】(1)(0,2);(2)BD=2AF;(3)OC=OB+AF.
【解析】试题分析:(1)只要求出Rt△ADC≌Rt△COB即可求.
(2)先说明BD与AE有怎样的数量关系,然后针对得到的数量关系,作出合适的辅助线,画出相应的图形,根据等腰三角形底边上的高、底边上的中线、顶角的平分线三线合一,可以最终证得所要说明的数量关系;
(3)先猜想OC、AF、OB之间的关系,然后根据猜想作出合适的辅助线,画出相应的图形,然后证明所要证明的结论即可.
试题解析:(1)∵点C坐标是(1,0),点A的坐标是(3,1)
∴AD=OC,
在Rt△ADC和Rt△COB中, ![]() ,
,
∴Rt△ADC≌Rt△COB(HL),
∴OB=CD=2,
∴点B的坐标是(0,2);
(2)BD=2AF,
理由:作AE的延长线交BC的延长线于点F,如下图所示,

∵△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,AE⊥y轴于E,
∴∠BCA=∠ACF=90°,∠AED=90°,
∴∠DBC+∠BDC=90°,∠DAE+∠ADE=90°,
∵∠BDC=∠ADE,
∴∠DBC=∠FAC,
在△BDC和△AFC中,
 ,
,
∴△BDC≌△AFC(ASA)
∴BD=AF,
∵BE⊥AE,y轴恰好平分∠ABC,
∴AF=2AE,
∴BD=2AF;
(3)OC=OB+AF,
证明:作AE⊥OC于点E,如下图所示,

∵AE⊥OC,AF⊥y轴,
∴四边形OFAE是矩形,∠AEC=90°,
∴AF=OE,
∵△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,∠BOC=90°,
∴∠BCA=90°,
∴∠BCO+∠CBO=90°,∠BCO+∠ACE=90°,
∴∠CBO=∠ACE,
在△BOC和△CEO中,
 ,
,
∴△BOC≌△CEO(AAS)
∴OB=CE,
∵OC=OE+EC,OE=AF,OB=EC,
∴OC=OB+AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)求证:EG=FG.
(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式2(﹣2)=0成立,则“”内的运算符号是( ).
A.+B.﹣C.×D.÷
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数是甲组人数的2倍还多1人.从甲组抽调了多少学生去乙组?
-
科目: 来源: 题型:
查看答案和解析>>【题目】据有关资料显示,长江三峡工程电站的总装机容量是18200000千瓦,请你用科学记数法表示电站的总装机容量,应记为千瓦.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=x+b的图象经过第一、三、四象限,则b的值可以是( )
A. ﹣1 B. 0 C. 1 D. 2
-
科目: 来源: 题型:
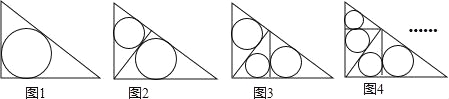
查看答案和解析>>【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .
相关试题

