【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)求证:EG=FG.
(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

参考答案:
【答案】(1)证明见解析(2)成立
【解析】试题分析:(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DEG,从而得出GE=GF;
(2)结论仍然成立,同理可以证明得到.
试题解析:(1)证明:∵DE⊥AC,BF⊥AC,
∴∠DEF=∠BFE=90°.
∵AE=CF,AE+EF=CF+EF.即AF=CE.
在Rt△ABF和Rt△CDE中, ![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFG和△DEG中, 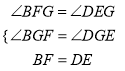 ,
,
∴△BFG≌△DGE(AAS),
∴GE=GF;
(2)结论依然成立.
理由:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°
∵AE=CF
∴AE﹣EF=CF﹣EF,即AF=CE,
在Rt△ABF和Rt△CDE中, ![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF
在△BFG和△DEG中, 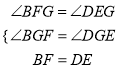 ,
,
∴△BFG≌△DGE(AAS),
∴GE=GF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(a,-1)与点N(2,b)关于y轴对称,则a+b的值是( )
A. 3 B. -3 C. 1 D. -1
-
科目: 来源: 题型:
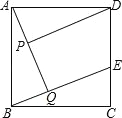
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式2(﹣2)=0成立,则“”内的运算符号是( ).
A.+B.﹣C.×D.÷
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数是甲组人数的2倍还多1人.从甲组抽调了多少学生去乙组?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=AC,∠C=90°,直角顶点C在x轴上,一锐角顶点B在y轴上.
(1)如图①若AD于垂直x轴,垂足为点D.点C坐标是(﹣1,0),点A的坐标是(﹣3,1),求点B的坐标.
(2)如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,请猜想BD与AE有怎样的数量关系,并证明你的猜想.
(3)如图③,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,请猜想OC,AF,OB之间有怎样的关系(直接写出结论,不需要证明)

相关试题

