【题目】A，B两地相距60 km，甲、乙两人从两地出发相向而行，甲先出发．图中l1，l2表示两人离A地的距离s(km)与时间t(h)的关系，请结合图象解答下列问题：

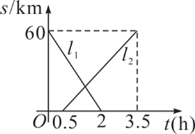
(1)表示乙离A地的距离与时间关系的图象是_____(填l1或l2)；甲的速度是_____，乙的速度是_____

(2)甲出发多少小时两人恰好相距5 km?

参考答案：

【答案】(1) l2， 30km/h，20km/h；(2) 1.3或1.5

【解析】

（1）因为甲先出发，所以l1，l2分别表示甲、乙的函数图象，速度可以根据路程与时间的关系得到；

（2）出发后两人恰好相距5km的情况要分类讨论，分相遇前与相遇后考虑，列方程即可解决．

解：（1）∵甲先出发，由图象可知l2表示乙的函数图象

v甲=60÷2=30，v乙=60÷（3.5-0.5）=20

故答案为l2，30，20．

（2）设l1对应的函数解析式为s1=k1t+b1，l2对应的函数解析式为s2=k2t+b2，

将（0，60），（2，0）代入s1=k1t+b1中

利用待定系数法，可得s1=-30t+60，

将（0.5，0），（3.5，60）代入s2=k2t+b2中

利用待定系数法，可得s2=20t-10，

设甲出发x小时两人恰好相距5km．

由题意:

相遇前：30x+20(x-0.5)+5=60 x=1.3

相遇后：30x+20(x-0.5)-5=60 x=1.5

答：甲出发1.3小时或1.5小时两人恰好相距5km．

关闭