【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.

解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线![]() :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
参考答案:
【答案】(1)y=—2x+6,直线的图象如图:
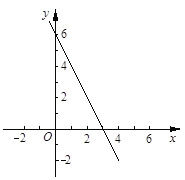
(2)△![]() 的面积
的面积![]() 关于的函数表达式为
关于的函数表达式为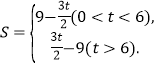
【解析】
试题(1)设直线l的函数表达式为y=k x+b,根据平行的性质可得k=—2,再根据直线l过点(1,4),即可求得直线l的函数表达式,最后根据描点法即可做出直线的图象;
(2)先分别求得直线l分别与y轴、x轴的交点A、B的坐标,再根据l∥![]() ,可设直线
,可设直线![]() 为y=—2x+t,从而表示出C点的坐标为(
为y=—2x+t,从而表示出C点的坐标为(![]() ,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
(1)设直线l的函数表达式为y=k x+b.
∵直线l与直线y=—2x—1平行,∴k=—2.
∵直线l过点(1,4),∴—2+b=4,∴b=6.
∴直线l的函数表达式为y=—2x+6,直线的图象如图:
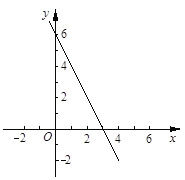
(2)∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,6)、(3,0).
∵l∥![]() ,∴直线
,∴直线![]() 为y=—2x+t.
为y=—2x+t.
∴C点的坐标为(![]() ,0).
,0).
∵t>0,
∴![]() >0.
>0.
∴C点在x轴的正半轴上.
当C点在B点的左侧时,![]() ;
;
当C点在B点的右侧时,![]() .
.
∴△![]() 的面积
的面积![]() 关于的函数表达式为
关于的函数表达式为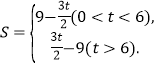
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年元月,国内一家网络诈骗举报平台发布了《2015年网络诈骗趋势研究报告》,根据报告提供的数据绘制了如下的两幅统计图:
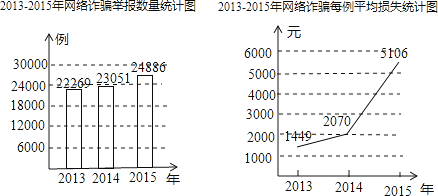
(1)该平台2015年共收到网络诈骗举报多少例?
(2)2015年通过该平台举报的诈骗总金额大约是多少亿元?(保留三个有效数字)
(3)2015年每例诈骗的损失年增长率是多少?
(4)为提高学生的防患意识,现准备从甲、乙、丙、丁四人中随机抽取两人作为受骗演练对象,请用树状图或列表法求恰好选中甲、乙两人的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
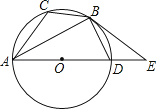
(1)求证:BE是⊙O的切线;
(2)若BC=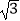 ,AC=5,求圆的直径AD及切线BE的长.
,AC=5,求圆的直径AD及切线BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠1=∠2.
(1)请你添加一个与直线AC有关的条件,由此可得出BE是△ABC的外角平分线;
(2)请你添加一个与∠1有关的条件,由此可得出BE是△ABC的外角平分线;
(3)如果“已知在△ABC中,∠1=∠2不变”,请你把(1)中添加的条件与所得结论互换,所得的命题是否是真命题,理由是什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.

(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )

A. 5对; B. 4对; C. 3对; D. 2对
-
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
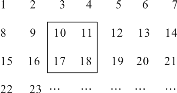
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
相关试题

