Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到点C时，两点都停止．设运动时间为t秒．

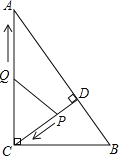
（1）求线段CD的长；

（2）当t取何值时PQ∥AB？

（3）是否存在某一时刻t，使得△PCQ为等腰三角形？若存在，求出所有满足条件的t的值；若不存在，请说明理由．

Answer 1

【答案】（1）4.8；（2）当t=3时，PQ∥AB；（3）当t为2.4秒或秒或秒时，△CPQ为等腰三角形．

【解析】

试题分析：（1）先根据勾股定理求出AB的长，再由三角形的面积公式即可得出结论；

（2）先用t表示出DP，CQ，CP的长，再根据PQ∥AB，得到△QCP∽△ABC，根据相似三角形的性质列方程即可得到结论；

（3）根据题意画出图形，分CQ=CP，PQ=PC，QC=QP三种情况进行讨论．

解：（1）∵∠ACB=90°，AC=8，BC=6，

∴AB=10．

∵CD⊥AB，

∴S△ABC=BCAC=ABCD．

∴CD===4.8．

∴线段CD的长为4.8．

（2）设DP=t，CQ=t．则CP=4.8﹣t．

∵PQ∥AB，

∵△QCP∽△ABC

∴，即，

∴t=3，

当t=3时，PQ∥AB；

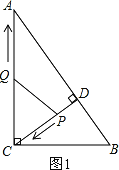
（3）①若CQ=CP，如图1，

则t=4.8﹣t．

解得：t=2.4．

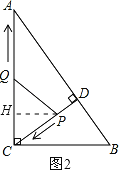
②若PQ=PC，如图2所示．

∵PQ=PC，PH⊥QC，

∴QH=CH=QC=．

∵△CHP∽△BCA．

∴，

∴=，解得t=；

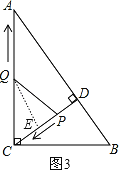
③若QC=QP，

过点Q作QE⊥CP，垂足为E，如图3所示．

同理可得：t=．

综上所述：当t为2.4秒或秒或秒时，△CPQ为等腰三角形．