【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角形的直角(∠MON=90°)顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
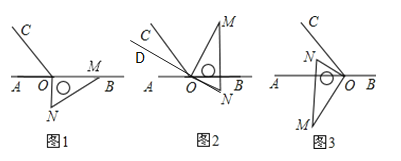
(1)在图1中,∠NOC= .
(2)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:NO的延长线OD是否平分∠AOC?请说明理由;
(3)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 秒?(直接写出结果)
(4)将图1中的三角板绕点O旋转至图3的位置,使ON在∠AOC的内部,则∠AOM-∠NOC= °
参考答案:
【答案】(1)150°;(2)![]() 平分
平分![]() ,理由详见解析;(3)
,理由详见解析;(3)![]() 或
或![]() ;(4)30
;(4)30
【解析】
(1)根据![]() 的度数求出
的度数求出![]() 的度数,然后利用
的度数,然后利用![]() 即可求解;
即可求解;
(2)根据角平分线的定义求出![]() ,进而求出
,进而求出![]() ,则有
,则有
![]() ,则说明
,则说明![]() 平分
平分![]() ;
;
(3)根据第(2)问可知图2时直线ON平分锐角![]() ,求出
,求出![]() 的度数即可求出时间;另一种情况是ON转到
的度数即可求出时间;另一种情况是ON转到![]() 的内部平分
的内部平分![]() ,求出此时相对于第一种情况又转过了多少度,经过了多长时间即可得出最后的结果;
,求出此时相对于第一种情况又转过了多少度,经过了多长时间即可得出最后的结果;
(4)根据![]() 的度数表示出
的度数表示出![]() 的度数,然后利用
的度数,然后利用![]() 即可求解.
即可求解.
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 平分
平分![]() .理由如下:
.理由如下:
![]()
![]()
![]() 平分
平分![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() 平分
平分![]() ;
;
![]() 由
由![]() 可知,当
可知,当![]() 时,直线
时,直线![]() 平分锐角
平分锐角![]() ,此时
,此时![]() ;
;
另外一种情况是ON转到![]() 的内部平分
的内部平分![]() ,即相对于图(2)时ON又转过
,即相对于图(2)时ON又转过![]() ,所以又过了
,所以又过了![]() ,所以当ON再次
,所以当ON再次![]() 平分锐角
平分锐角![]() 时,
时,![]()
直线ON恰好平分锐角∠AOC时,![]() 或
或![]() 秒.
秒.
(4)![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
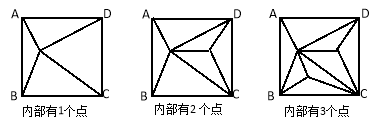
(1)填写下表:
正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有_____.(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).
问:(1)设购买乒乓球x盒时,在甲家购买所需多少元?在乙家购买所需多少元?(用含x的代数式表示,并化简)
(2)当购买乒乓球多少盒时,两种优惠办法付款一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的腰长为2,直角顶点A在直线l:y=2x+2上移动,且斜边BC∥x轴,当△ABC在直线l上移动时,BC的中点D满足的函数关系式为( )

A. y=2x B. y=2x+1 C. y=2x+2﹣
 D. y=2x﹣
D. y=2x﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为
 米,广场的长为
米,广场的长为 米,宽为
米,宽为 米.
米.(1)请列式表示花坛的面积和广场空地的面积;
(2)若休闲广场的长为500米,宽为200米,圆形花坛的半径为20米,求广场空地的面积;(计算结果保留
 ;
;(3)在(2)的情况下,若
 取3.14,求休闲广场的绿化率是多少?
取3.14,求休闲广场的绿化率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标系下画出函数
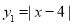 的图像,
的图像,
(1)正比例函数
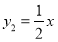 的图像与
的图像与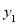 图像交于A,B两点,A在B的左侧,画出
图像交于A,B两点,A在B的左侧,画出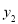 的图像并求A,B两点坐标
的图像并求A,B两点坐标(2)根据图像直接写出
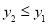 时自变量x的取值范围
时自变量x的取值范围(3)
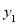 与x轴交点为C,求
与x轴交点为C,求 的面积
的面积
相关试题

