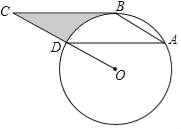
【题目】如图所示,点ABD都在⊙O上,BC是⊙O的切线,AD∥BC,∠C=30°,AD=4![]() .
.
(1)求∠A的度数;
(2)求由线段BC、CD与弧BD所围成的阴影部分的面积.(结果保留π)
参考答案:
【答案】(1)30°(2)![]()
【解析】分析:(1)连接OB,根据切线的性质求出∠OBC,根据三角形内角和定理求出∠BOC,根据圆周角定理推出即可;
(2)求出DM,解直角三角形求出OD,分别求出△OBC的面积和扇形DOB的面积,即可得出答案.
详解:(1)连接OB,交AD于M,
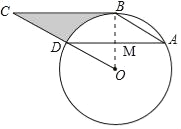
∵BC为⊙O切线,
∴∠OBC=90°,
∵∠C=30°,∠OBC=90°,
∴∠BOD=60°,
∴∠A=![]() ;
;
(2)∵AD∥BC,∠OBC=90°,
∴∠OMD=∠OBC=90°,
∴由垂径定理得DM=![]() ,
,
∵Rt△OMD中,DM=2![]() ,∠BOD=60°,
,∠BOD=60°,
∴OD=![]() ,
,
在Rt△OBC中,OB=4,∠BOC=60°,
∴BC=OB×tan∠BOC=4×tan60°=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴阴影部分的面积=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
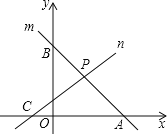
(1)如图,3x+3y=12,的图象为直线m,其与x轴交点A的坐标为____,其与y轴交点B的坐标为___;
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-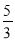 ,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算a
 b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:①2
 (-2)=6 ②a
(-2)=6 ②a b=b
b=b a
a③若a+b=0,则(a
 a)+(b
a)+(b b)=2ab ④若a
b)=2ab ④若a b=0,则a=0.
b=0,则a=0.其中正确结论的序号是 (填上你认为所有正确结论的序号).
-
科目: 来源: 题型:
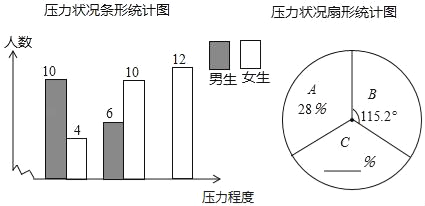
查看答案和解析>>【题目】中考科目已经发生变革,继中考增加体育实验之后,从2019年开始河南中考开始增设生物和地理科目,针对于此学校教务处王老师负责调查学生对此变革是否有压力,设置问题答案如下(A:大,B:一般,C:无),再将调查结果制成两幅不完统计图(如图所示),请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图和扇形统计图补充完整;
(3)为了缓解学生压力,王老师从被调查的A类和B类学生中分别选取一名学生进行详细心理调查,请用合适的方法恰好选中一名男生和一名学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
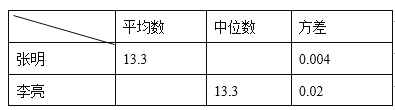
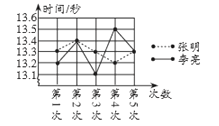
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
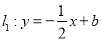 分别与
分别与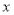 轴,
轴, 轴交于
轴交于 两点,与直线
两点,与直线 交于点
交于点 .
.(1)点
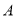 的坐标为__________,点
的坐标为__________,点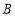 的坐标为__________
的坐标为__________(2)在线段
 上有一点
上有一点 ,过点
,过点 作
作 轴的平行线
轴的平行线 交直线
交直线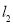 于点
于点 ,设点
,设点 的横坐标为
的横坐标为 ,当
,当 为何值时,四边形
为何值时,四边形 是平行四边形.
是平行四边形.
-
科目: 来源: 题型:
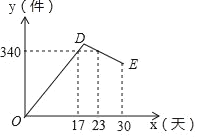
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
相关试题

