【题目】如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________
的坐标为__________
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形.
是平行四边形.

参考答案:
【答案】(1)(8,0) , (0,4) ;(2)当m为![]() 时,四边形OBEF是平行四边形.
时,四边形OBEF是平行四边形.
【解析】
(1)由点C的坐标利用待定系数法即可求出直线![]() 的解析式,再分别令直线
的解析式,再分别令直线![]() 的解析式中x=0、y=0求出对应的y、x值,即可得出点A、B的坐标;
的解析式中x=0、y=0求出对应的y、x值,即可得出点A、B的坐标;
(2)由点C的坐标利用待定系数法即可求出直线![]() 的解析式,结合点E的横坐标即可得出点E、F的坐标,再根据平行四边形的性质即可得出关于m的一元一次方程,解方程即可得出结论;
的解析式,结合点E的横坐标即可得出点E、F的坐标,再根据平行四边形的性质即可得出关于m的一元一次方程,解方程即可得出结论;
解:(1)将点C(4,2)代入y=![]() x+b中,
x+b中,
得:2=2+b,解得:b=4,
∴直线![]() 为y=
为y=![]() x+4.
x+4.
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴B(0,4);
令y=![]() x+4中y=0,则x=8,
x+4中y=0,则x=8,
∴A(8,0).
故答案为:(8,0)(0,4)
(2)将C(4,2)分别代入y=-![]() x+b, y=kx-6,得b=4,k=2.
x+b, y=kx-6,得b=4,k=2.
∴直线l1的解析式为y=-![]() x+4,直线l2的解析式为y=2x-6.
x+4,直线l2的解析式为y=2x-6.
∵点E的横坐标为m,
∴点E的坐标为(m,-![]() m+4),点F的坐标为(m,2m-6).
m+4),点F的坐标为(m,2m-6).
∴EF=-![]() m+4-(2m-6)=-
m+4-(2m-6)=-![]() m+10.
m+10.
∵四边形OBEF是平行四边形,
∴EF=OB,即-![]() m+10=4.
m+10=4.
解得m=![]() .
.
∴当m为![]() 时,四边形OBEF是平行四边形.
时,四边形OBEF是平行四边形.
-
科目: 来源: 题型:
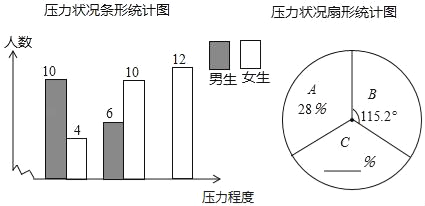
查看答案和解析>>【题目】中考科目已经发生变革,继中考增加体育实验之后,从2019年开始河南中考开始增设生物和地理科目,针对于此学校教务处王老师负责调查学生对此变革是否有压力,设置问题答案如下(A:大,B:一般,C:无),再将调查结果制成两幅不完统计图(如图所示),请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图和扇形统计图补充完整;
(3)为了缓解学生压力,王老师从被调查的A类和B类学生中分别选取一名学生进行详细心理调查,请用合适的方法恰好选中一名男生和一名学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点ABD都在⊙O上,BC是⊙O的切线,AD∥BC,∠C=30°,AD=4
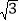 .
.(1)求∠A的度数;
(2)求由线段BC、CD与弧BD所围成的阴影部分的面积.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
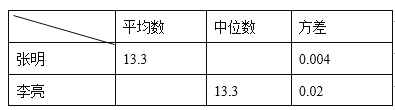
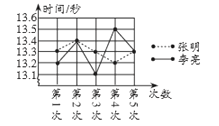
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
-
科目: 来源: 题型:
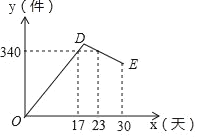
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路
 的一侧点
的一侧点 处有一村庄,村庄
处有一村庄,村庄 到公路
到公路 的距离为800米,假使宣讲车
的距离为800米,假使宣讲车 周围1000米以内能听到广播宣传,宣讲车
周围1000米以内能听到广播宣传,宣讲车 在公路
在公路 上沿
上沿 方向行驶时:
方向行驶时:
(1)请问村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
-
科目: 来源: 题型:
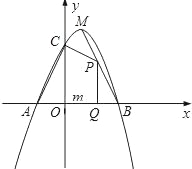
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.
相关试题

