搜索
【题目】如图，
是四边形
的对角线，AD//BC，
，分别过点
作
、
，垂足分别为点
，若
，则图中全等的三角形有（ ）
A.
对B.
对C.
对D.
对
参考答案：
【答案】C
【解析】
求出DE=BF，根据平行线性质求出∠ADE=∠CBF，根据ASA推出△ADE≌△CBF，推出AE=CF，根据SAS推出△ABE≌△CDF，推出AD=BC，根据SAS推出△ADB≌△CBD即可．
解：∵BD=BD，BE=DF，
∴DE=BF，
∵AD∥BC，
∴∠ADE=∠CBF，
在△ADE和△CBF中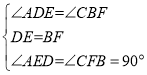
∴△ADE≌△CBF（ASA），
∴AE=CF，
在△ABE和△CDF中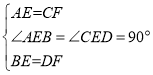
∴△ABE≌△CDF（SAS），
∴AD=BC
在△ADB和△CBD中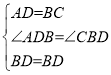
∴△ADB≌△CBD（SAS），
即有3对全等三角形，
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有一座拱桥是圆弧形，它的跨度AB=60米，拱高PD=18米．
（1）求圆弧所在的圆的半径r的长；
（2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE=4米时，是否要采取紧急措施？
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究函数
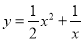的图象与性质，下面是探究过程，请补充完整：（
）下表是
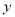与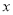
的几组对应值．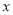
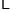
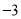
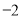
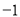
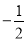
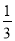
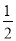
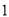
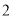
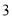
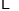
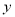
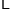
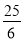
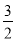
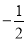
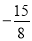
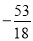
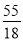
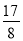
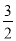
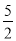
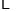
函数
的自变量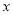
的取值范围是__________， 
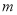的值为__________．（
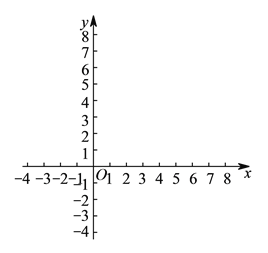
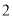）描出以上表中各对对应值为坐标的点，并画出该函数的大致图象．（
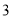）进一步探究函数图象发现：①函数图象与
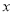轴有__________个交点，所以对应方程
有__________个实数根．②方程
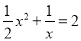有__________个实数根．③结合函数的图象，写出该函数的一条性质__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC＝2，∠B＝∠C＝40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE＝40°，DE交线段AC于E．
（1）当∠BDA＝115°时，∠EDC＝ °，∠DEC＝ °；点D从B向C运动时，∠BDA逐渐变 （填“大”或“小”）；
（2）当DC等于多少时，△ABD≌△DCE，请说明理由；
（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，如图②均是
的正方形网格，每个小正方形顶点叫做格点．
的顶点都在格点上．
（1）在如图①的网格中找到一个格点
，并画出
，使与全等，且以点
为顶点的四边形只是轴对称图形．（2）在如图②的网格中找到一个格点
，并画出
，使与全等，且以点
为顶点的四边形只是中心对称图形． -
科目： 来源： 题型：
查看答案和解析>>【题目】夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元.
（1）设第
天生产空调
台，直接写出与之间的函数解析式，并写出自变量的取值范围.（2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第
天的利润为
元，试求与
之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，有一块长为
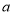米、宽为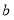
米的长方形空地，现计划将这块空地四周均留出2米宽修道路，中间用来绿化．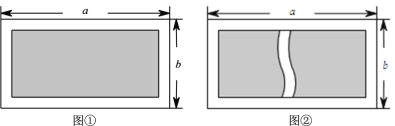
（1）求绿化的面积（用含
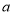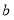、的代数式表示）．（2）若长方形空地的面积为576米2，周长为120米，求绿化的面积．
（3）若在图①的绿化部分再修一条2米宽道路，如图②，求绿化的面积（用含
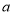、的代数式表示）．
相关试题
