【题目】探究函数![]() 的图象与性质,下面是探究过程,请补充完整:
的图象与性质,下面是探究过程,请补充完整:
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
函数![]() 的自变量
的自变量![]() 的取值范围是__________,
的取值范围是__________, ![]() 的值为__________.
的值为__________.
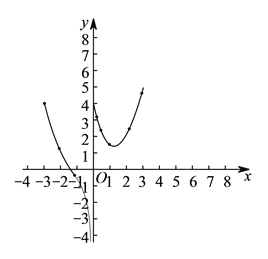
(![]() )描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
)描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
(![]() )进一步探究函数图象发现:
)进一步探究函数图象发现:
①函数图象与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有__________个实数根.
有__________个实数根.
②方程![]() 有__________个实数根.
有__________个实数根.
③结合函数的图象,写出该函数的一条性质__________.
参考答案:
【答案】(![]() )
)![]() ,
, ![]() ;(
;(![]() )图象见解析;(
)图象见解析;(![]() )①
)①![]() .
. ![]() ;②
;②![]() ;③函数没有最大值或函数没有最小值或函数图像没有经过第四象限(答案不唯一).
;③函数没有最大值或函数没有最小值或函数图像没有经过第四象限(答案不唯一).
【解析】试题分析:(1)根据分式的分母不为零确定出自变量x的取值范围为x≠1,把x=3代入函数的解析式求得m=![]() ;(2)在坐标系中描出根据表中各对对应值为坐标的点,连接画出函数图象即可;(3)①观察图象即可得:函数图象与
;(2)在坐标系中描出根据表中各对对应值为坐标的点,连接画出函数图象即可;(3)①观察图象即可得:函数图象与![]() 轴有1个交点,所以对应方程
轴有1个交点,所以对应方程![]() 有1个实数根;②观察图象即可得方程
有1个实数根;②观察图象即可得方程![]() 有3个实数根;③根据函数图象写出该函数的一条性质即可,答案不唯一,正确即可.
有3个实数根;③根据函数图象写出该函数的一条性质即可,答案不唯一,正确即可.
试题解析:
(![]() )由题意可得
)由题意可得![]() ,
, ![]() ,故答案为
,故答案为![]() ,
, ![]() .
.
(![]() )如图所示.
)如图所示.
(![]() )①
)①![]() .
. ![]() .
.
②![]() .
.
③函数没有最大值或函数没有最小值或函数图像没有经过第四象限(答案不唯一).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年年初,新型冠状病毒在武汉等地区肆虐,为了缓解湖北地区的疫情,全国各地的医疗队员都纷纷报名支援湖北,某方舱医院需要8组医护人员支援,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人,若每组人数比预定人数少分配一人,则总数不够90人,那么预定每组分配的人数是多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC.
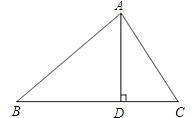
(1)求证:AC=BD;
(2)若sin∠C=
 ,BC=12,求AD的长.
,BC=12,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是四边形
是四边形 的对角线,AD//BC,
的对角线,AD//BC, ,分别过点
,分别过点 作
作 、
、 ,垂足分别为点
,垂足分别为点 ,若
,若 ,则图中全等的三角形有( )
,则图中全等的三角形有( )
A.
 对B.
对B. 对C.
对C. 对D.
对D. 对
对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,如图②均是
 的正方形网格,每个小正方形顶点叫做格点.
的正方形网格,每个小正方形顶点叫做格点. 的顶点都在格点上.
的顶点都在格点上.
(1)在如图①的网格中找到一个格点
 ,并画出
,并画出 ,使
,使 与
与 全等,且以点
全等,且以点 为顶点的四边形只是轴对称图形.
为顶点的四边形只是轴对称图形.(2)在如图②的网格中找到一个格点
 ,并画出
,并画出 ,使
,使 与
与 全等,且以点
全等,且以点 为顶点的四边形只是中心对称图形.
为顶点的四边形只是中心对称图形.
相关试题

