搜索
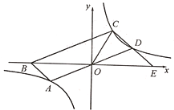
【题目】如图，在平面直角坐标系中，平行四边形ABCD的边AD经过O点，A、C、D三点都在反比例函数
的图像上，B点在
轴的负半轴上，延长CD交轴于点E，连接CO.
若C（1,2）,D(2,1)，则
为_______.
参考答案：
【答案】6
【解析】
根据C,D的坐标可求出S△CDO的值，再根据平行四边形的性质得出△AOB≌△DOE，故OD为△CEO的中线，则可求出△COE的面积，再利用平行四边形ABCD的面积等于△BEC的面积即可求解.
延长CD交x轴与点E，
∵C（1,2）,D(2,1)，
∴S△CDO=
=
∵四边形ABCD为平行四边形，A,D关于原点对称，∴△AOB≌△DOE，
故D点为CE中点，则S△COE=2S△CDO=3，
又O点为BE中点，
故
=S△BEC=2S△COE=6
-
科目： 来源： 题型：
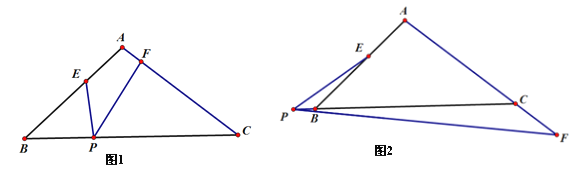
查看答案和解析>>【题目】（1）如图1，△ABC中，∠BAC=100°，AB=AC，P为BC边上任意一点.若点E、F分别在AB、AC上，且∠EPF=40°，求证：△BPE∽△CFP；
（2）如图2，点P在边CB的延长线上，点E在边AB上，点F在边AC的延长线上，仍有∠EPF=40°，探索PB·PC与BE·CF有怎样的关系？并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AC＝BC，AB⊥x轴，垂足为A.反比例函数y＝
(x＞0)的图象经过点C，交AB于点D.已知AB＝4，BC＝
.(1)若OA＝4，求k的值；
(2)连接OC，若BD＝BC，求OC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．
（1）在图1中，画出一个与△ABC成中心对称的格点三角形；
（2）在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；
（3）在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形；
（4）在图4中，画出所有格点△BCD，使△BCD为等腰直角三角形，且S△BCD=4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校计划组织师生共300人参加一次大型公益活动，如果租用6辆大客车和5辆小客车，恰好全部坐满，已知每辆大客车的乘客座位数比小客车多17个．
（1）求每辆大客车和每辆小客车的乘客座位数；
（2）由于最后参加活动的人数增加了30人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，且所有参加活动的师生都有座位，求租用小客车数量的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D、E分别是等边三角形ABC的边BC、AC上的点，连接AD、BE交于点O，且△ABD≌△BCE．
（1）若AB=3，AE=2，则BD= ；
（2）若∠CBE=15°，则∠AOE= ；
（3）若∠BAD=a，猜想∠AOE的度数，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】课堂上李老师给出了一道整式求值的题目，李老师把要求的整式（7a3-6a3b+3a2b）-（-3a3-6a3b+3a2b+10a3-3）写完后，让王泓同学顺便给出一组
的值，老师自己说答案，当王泓说完：“
”后，李老师不假思索，立刻就说出答案：“3”。同学们觉得不可思议，李老师用坚定的口吻说：“这个答案准确无误。”聪明的同学们，你能说出其中的道理吗？
相关试题
