【题目】已知线段![]()

(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向点
向点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 沿线段点
沿线段点![]() 向点
向点![]() 以
以![]() 的速度运动,几秒钟后,
的速度运动,几秒钟后,![]() 两点相遇?
两点相遇?
(2)如图1,几秒后,点![]() 两点相距
两点相距![]() ?
?
(3)如图2,![]() ,
,![]() ,当点
,当点![]() 在
在![]() 的上方,且
的上方,且![]() 时,点
时,点![]() 绕着点
绕着点![]() 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 两点能相遇,求点
两点能相遇,求点![]() 的运动速度.
的运动速度.
参考答案:
【答案】(1)6秒钟;(2)4秒钟或8秒钟;(3)点![]() 的速度为
的速度为![]() 或
或![]() .
.
【解析】
(1)设经过![]() 后,点
后,点![]() 相遇,根据题意可得方程
相遇,根据题意可得方程![]() ,解方程即可求得t值;(2)设经过
,解方程即可求得t值;(2)设经过![]() ,
,![]() 两点相距
两点相距![]() ,分相遇前相距10cm和相遇后相距10cm两种情况求解即可;(3)由题意可知点
,分相遇前相距10cm和相遇后相距10cm两种情况求解即可;(3)由题意可知点![]() 只能在直线
只能在直线![]() 上相遇,由此求得点Q的速度即可.
上相遇,由此求得点Q的速度即可.
解:(1)设经过![]() 后,点
后,点![]() 相遇.
相遇.
依题意,有![]() ,
,
解得:![]() .
.
答:经过6秒钟后,点![]() 相遇;
相遇;
(2)设经过![]() ,
,![]() 两点相距
两点相距![]() ,由题意得
,由题意得
![]() 或
或![]() ,
,
解得:![]() 或
或![]() .
.
答:经过4秒钟或8秒钟后,![]() 两点相距
两点相距![]() ;
;
(3)点![]() 只能在直线
只能在直线![]() 上相遇,
上相遇,
则点![]() 旋转到直线
旋转到直线![]() 上的时间为:
上的时间为:![]() 或
或![]() ,
,
设点![]() 的速度为
的速度为![]() ,则有
,则有![]() ,
,
解得:![]() ;
;
或![]() ,
,
解得![]() ,
,
答:点![]() 的速度为
的速度为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)13×(﹣5)
(2)(﹣21)÷(﹣7)
(3)﹣3+(﹣5)﹣(﹣7)
(4)(﹣36
 )÷9.
)÷9.(5)11
 ﹣(
﹣( +2
+2 )
) (6)
 ÷1
÷1 ×3
×3 .
. (7)(﹣0.5)+|0﹣6
 |﹣(﹣7
|﹣(﹣7 )﹣(﹣4.75)
)﹣(﹣4.75) (8)99
 ×(﹣9)
×(﹣9) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=-x+2的图象与反比例函数y2=
 的图象相交于A,B两点,点B的坐标为(2m,-m).
的图象相交于A,B两点,点B的坐标为(2m,-m).
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<2m时,y2的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区的手机收费如下
 两种方式(接听均免费),用户可任选其一:
两种方式(接听均免费),用户可任选其一:A:月租费0元,拨打电话计费0.15元/分
B:月租费15元,拨打电话计费0.1元/分
(1)某用户某月打手机100分钟,请计算两种方式各缴费多少元?
(2)某用户某月打手机x分钟,请你写出两种方式下该用户应缴付的费用?
(3)若某用户估计一个月内打手机15小时,你认为哪种方式更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市实施居民用水阶梯价格制度,按年度用水量计算,将居民家庭全年用水量划分为三个阶梯,水价按阶梯递增:
第一阶梯:年用水量不超过200吨,每吨水价为3元;
第二阶梯:年用水量超过200吨但不超过300吨的部分,每吨水价为3. 5元;
第三阶梯:年用水量超过300吨的部分,每吨水价为6元.
(1)小明家2018年用水180吨,这一年应缴纳水费 元;
(2)小亮家2018年缴纳水费810元,则小亮家这一年用水多少吨?
(3)小红家2017年和2018年共用水600吨,共缴纳水费1950元,并且2018年的用水量超过2017年的用水量,则小红家2017年和2018年各用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本,并且所购买A笔记本的数量要不多于B笔记本数量的
 ,但又不少于B笔记本数量
,但又不少于B笔记本数量 ,设买A笔记本n本,买两种笔记本的总费为w元.
,设买A笔记本n本,买两种笔记本的总费为w元.(1)写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
(2)购买这两种笔记本各多少时,费用最少?最少的费用是多少元?
(3)商店为了促销,决定仅对A种类型的笔记本每本让利a元销售,B种类型笔记本售价不变.问购买这两种笔记本各多少本时花费最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在线段
在线段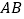 上.点
上.点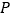 从点
从点 出发向点
出发向点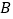 运动,速度为2cm/s;同时,点
运动,速度为2cm/s;同时,点 也从点
也从点 出发用1s到达
出发用1s到达 处,并在
处,并在 处停留2s,然后按原速度向点
处停留2s,然后按原速度向点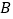 运动,速度为4cm/s.最终,点
运动,速度为4cm/s.最终,点 比点
比点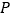 早1s到达
早1s到达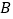 处.设点
处.设点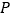 运动的时间为
运动的时间为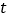 s.
s.(1)线段
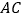 的长为 cm;当
的长为 cm;当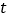 =3s时,
=3s时,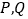 两点之间的距离为 cm;
两点之间的距离为 cm;(2)求线段
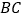 的长;
的长;(3)从
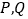 两点同时出发至点
两点同时出发至点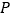 到达点
到达点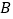 处的这段时间内,
处的这段时间内,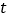 为何值时,
为何值时, 两点相距1 cm?
两点相距1 cm?
相关试题

