【题目】如图,点![]() 在线段
在线段![]() 上.点
上.点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,速度为2cm/s;同时,点
运动,速度为2cm/s;同时,点![]() 也从点
也从点![]() 出发用1s到达
出发用1s到达![]() 处,并在
处,并在![]() 处停留2s,然后按原速度向点
处停留2s,然后按原速度向点![]() 运动,速度为4cm/s.最终,点
运动,速度为4cm/s.最终,点![]() 比点
比点![]() 早1s到达
早1s到达![]() 处.设点
处.设点![]() 运动的时间为
运动的时间为![]() s.
s.
(1)线段![]() 的长为 cm;当
的长为 cm;当![]() =3s时,
=3s时,![]() 两点之间的距离为 cm;
两点之间的距离为 cm;
(2)求线段![]() 的长;
的长;
(3)从![]() 两点同时出发至点
两点同时出发至点![]() 到达点
到达点![]() 处的这段时间内,
处的这段时间内,![]() 为何值时,
为何值时,![]() 两点相距1 cm?
两点相距1 cm?
![]()
参考答案:
【答案】(1)20,10;(2)CB=16cm;(3)当P,Q两点同时出发至点P到达点B处的这段时间内,t为![]() ,
,![]() ,
,![]() ,或
,或![]() 时,P,Q两点相距1cm.
时,P,Q两点相距1cm.
【解析】
(1)用点P的运动时间表示出点Q的运动时间,在根据点P和点Q从C-B的距离相等列出方程求出t;
(2)在(1)的基础上求出t后带入其中一个代数式即可求出CB的距离;
(3)已知点P,Q的速度,根据数轴的特点,分为四种情况下讨论PQ的位置特点,在结合两点之间的距离为1,根据时间×速度=路程,即可求出t的值.
(1)∵点P运动的时间为ts,
∴点Q运动的时间是(t-3),点P从C-B所走的路程为2t,
∵点Q先到了A点用时1s,又在点A处停留2s,
∴点Q从C-B所用时间是(t-1-1-2-1)=t-5,
∴点Q从C-B所走的路程为4(t-5),
∴2t=4(t-5),
解得t=10,
∴AC=4×1=4cm,BC=10×2=20,
当t=3时,点Q在点A处,
而CP=2×3=6cm,
∴PQ=AC+CP=4+6=10cm;
(2)由(1)知:当t=8时,CB=2t=2×8=16cm;
(3)①当点Q在AC上时,PQ=CP+CQ=4t+2t=1,解得t=![]() ;
;
②当点Q在CB上且在点P的左侧时,PQ=CP-CQ=2t-4(t-4)=1,解得t=![]() ;
;
③当点Q在CB上且在点P的右侧时,PQ=CQ-CP=4(t-4)-2t=1,解得t=![]() ;
;
④当点Q到达点B处时,PQ=CB-CP=20-2t=1,解得t=![]() .
.
答:当P,Q两点同时出发至点P到达点B处的这段时间内,t为![]() ,
,![]() ,
,![]() ,或
,或![]() 时,P,Q两点相距1cm.
时,P,Q两点相距1cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段


(1)如图1,点
 沿线段
沿线段 自点
自点 向点
向点 以
以 的速度运动,同时点
的速度运动,同时点 沿线段点
沿线段点 向点
向点 以
以 的速度运动,几秒钟后,
的速度运动,几秒钟后, 两点相遇?
两点相遇?(2)如图1,几秒后,点
 两点相距
两点相距 ?
?(3)如图2,
 ,
, ,当点
,当点 在
在 的上方,且
的上方,且 时,点
时,点 绕着点
绕着点 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点 沿直线
沿直线 自
自 点向
点向 点运动,假若点
点运动,假若点 两点能相遇,求点
两点能相遇,求点 的运动速度.
的运动速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市实施居民用水阶梯价格制度,按年度用水量计算,将居民家庭全年用水量划分为三个阶梯,水价按阶梯递增:
第一阶梯:年用水量不超过200吨,每吨水价为3元;
第二阶梯:年用水量超过200吨但不超过300吨的部分,每吨水价为3. 5元;
第三阶梯:年用水量超过300吨的部分,每吨水价为6元.
(1)小明家2018年用水180吨,这一年应缴纳水费 元;
(2)小亮家2018年缴纳水费810元,则小亮家这一年用水多少吨?
(3)小红家2017年和2018年共用水600吨,共缴纳水费1950元,并且2018年的用水量超过2017年的用水量,则小红家2017年和2018年各用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本,并且所购买A笔记本的数量要不多于B笔记本数量的
 ,但又不少于B笔记本数量
,但又不少于B笔记本数量 ,设买A笔记本n本,买两种笔记本的总费为w元.
,设买A笔记本n本,买两种笔记本的总费为w元.(1)写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
(2)购买这两种笔记本各多少时,费用最少?最少的费用是多少元?
(3)商店为了促销,决定仅对A种类型的笔记本每本让利a元销售,B种类型笔记本售价不变.问购买这两种笔记本各多少本时花费最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师给爱好学习的小兵和小鹏提出这样一个问题:如图1,在△ABC中,AB=AC点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小兵的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小鹏的证明思路是:如图2,过点P作PG⊥CF,垂足为G,先证△GPC≌△ECP,可得:PE=CG,而PD=GF,则PD+PE=CF.
请运用上述中所证明的结论和证明思路完成下列两题:
(1)如图3,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=16,CF=6,求PG+PH的值;
(2)如图4,P是边长为6的等边三角形ABC内任一点,且PD⊥AB,PF⊥AC,PE⊥BC,求PD+PE+PF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在△ABC中,∠A=30°,∠C=105°,AC=2
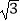 ,求AB的长.
,求AB的长.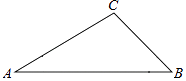
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明上星期买进某公司股票7000股,每股27元,下表为本周每日该股票的涨跌情况
 单位:元
单位:元
星期
一
二
三
四
五
六
每股涨跌






 这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的?
这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的? 哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗?
哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗? 本周六收盘时每股是多少元?
本周六收盘时每股是多少元?
相关试题

