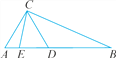
【题目】如图,在△ABC中,AD=AC,BE=BC.
(1)若∠ACB=96°,求∠DCE的度数.
(2)问:∠DCE与∠A,∠B之间存在怎样的数量关系(直接写出答案)?
参考答案:
【答案】(1)42°(2)∠DCE=![]() (∠A+∠B)
(∠A+∠B)
【解析】试题分析:(1)先由等边对等角的性质和三角形内角和定理得出∠A,∠B,∠ACB+∠A+∠B,然后等量代换求出∠DCE;
(2)由(1)可知∠DCE=180°-(∠CED+∠CDE),再由∠A=180°-2∠CDE,∠B=180°-2∠CED,得出∠1=90°-![]() ∠B,∠2=90°-
∠B,∠2=90°-![]() ∠A,将它们代入即可得出∠DCE=
∠A,将它们代入即可得出∠DCE=![]() (∠A+∠B),即可得到∠A,∠B与∠DCE之间的数量关系.
(∠A+∠B),即可得到∠A,∠B与∠DCE之间的数量关系.
试题解析:(1)∵AD=AC,
∴∠ADC=∠ACD.
∴∠A=180°-2∠ADC.
∵BE=BC,
∴∠CEB=∠ECB.
∴∠B=180°-2∠CEB.
∵∠ACB=96°,∴∠A+∠B=84°.
∴(180°-2∠ADC)+(180°-2∠CEB)=84°.
∴∠CEB+∠ADC=138°.∴∠DCE=42°.
(2)∠DCE=![]() (∠A+∠B).
(∠A+∠B).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a﹣5|+(b+2)2=0,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D、E为垂足,BD与CE交于点O,则图中全等三角形共有_________对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在Rt△ABC 中,
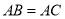 ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△ 绕点
绕点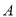 逆时针旋转90后,得到△
逆时针旋转90后,得到△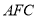 ,连接
,连接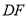 .
.(1)试说明:△
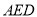 ≌△
≌△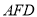 ;
; (2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
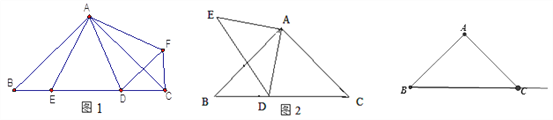
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,两条不重合直线的位置关系可能是( )
A.平行或相交
B.垂直或相交
C.垂直或平行
D.平行、垂直或相交 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解同学们平均每月阅读课外书籍的情况,在某年级随机抽查了20名同学,结果如下表所示:
平均每月阅读本数
4
5
6
7
8
人数
2
6
5
4
3
这些同学平均每月阅读课外书籍本数的中位数和众数为( )
A. 5,5B. 6,6C. 5,6D. 6,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形属于因式分解的是( )
A. (m-2)(m-3)=(3-m)(2-m) B. a2-2a+3=(a-1)2+2
C. (x+1)(x-1)=x2-1 D. 1-a2=(1+a)(1-a)
相关试题

