【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

参考答案:
【答案】![]() .
.
【解析】试题分析:作AD⊥BC,垂足为D,设CD=x,利用解直角三角形的知识,可得出AD,继而可得出BD,结合题意BC=CD+BD可得出方程,解出x的值后即可得出答案.
试题解析:如图,作AD⊥BC,垂足为D,
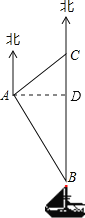
由题意得,∠ACD=45°,∠ABD=30°.
设CD=x,在Rt△ACD中,可得AD=x,
在Rt△ABD中,可得BD= ![]() ,
,
又∵BC=20(1+![]() ),CD+BD=BC,
),CD+BD=BC,
即x+ ![]() =20(1+
=20(1+![]() ),
),
解得:x=20,
∴AC=![]() x=20
x=20![]() (海里).
(海里).
答:A、C之间的距离为20![]() 海里.
海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场
优惠条件
甲商场
第一台按原价收费,其余的每台优惠25%
乙商场
每台优惠20%
(1)设学校购买
 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为 元,请分别求出
元,请分别求出 ,
, 与
与 之间的关系式.
之间的关系式.(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为
 元,从甲商场购买
元,从甲商场购买 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A的坐标为A(-1,0).
(1)画出△ABC平移后得到的
 使得点A的对应点
使得点A的对应点 的坐标为(2,-1),并写出
的坐标为(2,-1),并写出 的坐标;
的坐标;(2)画出△ABC绕点A顺时针旋转90°后得到的
 写出
写出 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABD中,AB=AD=1,∠B=30°,△ABD绕着A点逆时针α(0°<α<120°)旋转得到△ACE.CE与AD、BD分别交于点G、F;AD、CE交于点G,设DF+GF=x,△AEG的面积为y,则y关于x的函数解析式为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用两个完全相同的直角三角形纸片重叠在一起(如图1)固定△ABC不动,将△DEF沿线段AB向右平移.
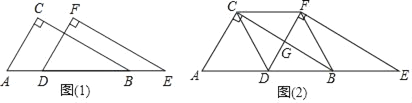
(1)若∠A=60°,斜边AB=4,设AD=x(0≤x≤4),两个直角三角形纸片重叠部分的面积为y,试求出y与x的函数关系式;
(2)在运动过程中,四边形CDBF能否为正方形,若能,请指出此时点D的位置,并说明理由;若不能,请你添加一个条件,并说明四边形CDBF为正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:角平分线上的点到这个角的两边的距离相等.
要求:(1)尺规作图:作∠AOB的角平分线,并在该角平分线上取点P,作PM⊥OA于点M,PN⊥OB于点N(不写作法,保留作图痕迹);
(2)以下是结合要证的命题和图形写出的已知,求证,请你完成证明过程.
已知:如图,OP平分∠AOB,PM⊥OA于点M,PN⊥OB于点N.
求证:PM=PN
证明:
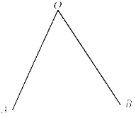
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了更好保障居民饮用水安全,环保局决定购10台污水处理设备,现有A、B两种型号的设备,价格与每台日处理污水的能力见下表.

(1)若县环保局购买污水处理设备的资金不超过105万元,你认为有哪几种方案.
(2)在(1)的条件下,每日要求处理污水量不低于2040吨,为了节约资金,请设计“一个最省钱”的购买方案.
相关试题

