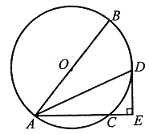
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E。
(1)求证:DE是⊙O的切线;
(2)求DE的长。
参考答案:
【答案】(1)详见解析;(2)4.
【解析】
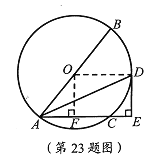
试题分析:(1)连结OD,由AD平分∠BAC,OA=OD,可证得∠ODA=∠DAE,由平行线的性质可得OD∥AE,再由DE⊥AC即可得OE⊥DE,即DE是⊙O的切线;(2)过点O作OF⊥AC于点F,由垂径定理可得AF=CF=3,再由勾股定理求得OF=4,再判定四边形OFED是矩形,即可得DE=OF=4.
试题解析:
(1)连结OD,
∵AD平分∠BAC,
∴∠DAE=∠DAB,
∵OA=OD,
∴∠ODA=∠DAO,
∴∠ODA=∠DAE,
∴OD∥AE,
∵DE⊥AC
∴OE⊥DE
∴DE是⊙O的切线;
(2)过点O作OF⊥AC于点F,
∴AF=CF=3,
∴OF=![]() ,
,
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形,
∴DE=OF=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)试说明:△ABC是直角三角形.
(2)请求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+30m表示向东走30m,那么向西走40m表示为( )
A.+40m
B.﹣40m
C.+30m
D.﹣30m -
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“平行于同一直线的两直线平行”写成“如果…,那么…”的形式 .
-
科目: 来源: 题型:
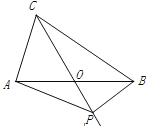
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC=
 ,求AF的长.
,求AF的长.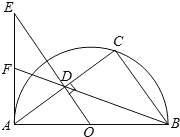
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校2 000名师生对我市 “三创”工作(创国家园林城市、国家卫生城市、全国文明城市)的知晓情况,从中随机抽取了100名师生进行问卷调查,这项调查中的样本是( )
A. 2 000名师生对“三创”工作的知晓情况
B. 从中抽取的100名师生
C. 从中抽取的100名师生对“三创”工作的知晓情况
D. 100
相关试题

