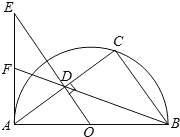
【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC=![]() ,求AF的长.
,求AF的长.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据已知条件易证△EAD∽△ABC,根据相似三角形的性质即可得结论;(2))作DM⊥AB于M,利用锐角三角函数和勾股定理分别求出DM、BM的长,再由DM∥AE,得![]() ,代入数据即可求得AF的长.
,代入数据即可求得AF的长.
试题解析:(1)证明:∵AB为半圆O的直径,
∴∠C=90°,
∵OD⊥AC,
∴∠CAB+∠AOE=90°,∠ADE=∠C=90°,
∵AE是切线,
∴OA⊥AE,
∴∠E+∠AOE=90°,
∴∠E=∠CAB,
∴△EAD∽△ABC,
∴AE:AB=AD:BC,
∴AEBC=ADAB.
(2)解:作DM⊥AB于M,
∵半圆O的直径为10,sin∠BAC=![]() ,
,
∴BC=ABsin∠BAC=6,
∴AC=![]() =8,
=8,
∵OE⊥AC,
∴AD=![]() AC=4,OD=
AC=4,OD=![]() BC=3,
BC=3,
∵sin∠MAD=![]() =
=![]() ,
,
∴DM=![]() ,AM=
,AM=![]() =
=![]() =
=![]() ,BM=AB﹣AM=
,BM=AB﹣AM=![]() ,
,
∵DM∥AE,
∴![]() ,
,
∴AF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“平行于同一直线的两直线平行”写成“如果…,那么…”的形式 .
-
科目: 来源: 题型:
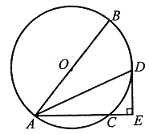
查看答案和解析>>【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E。
(1)求证:DE是⊙O的切线;
(2)求DE的长。
-
科目: 来源: 题型:
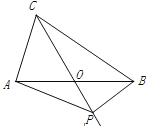
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校2 000名师生对我市 “三创”工作(创国家园林城市、国家卫生城市、全国文明城市)的知晓情况,从中随机抽取了100名师生进行问卷调查,这项调查中的样本是( )
A. 2 000名师生对“三创”工作的知晓情况
B. 从中抽取的100名师生
C. 从中抽取的100名师生对“三创”工作的知晓情况
D. 100
-
科目: 来源: 题型:
查看答案和解析>>【题目】在选取样本时,下列说法不正确的是( )
A. 所选样本必须足够大 B. 所选样本要具有代表性
C. 所选样本可按自己的爱好抽取 D. 仅仅增加调查人数不一定能提高调查质量
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(-3,-3),B(-2,-1),C(-1.-2)是坐标平面上三点.
(1)写出点C关于y轴的对称点C’的坐标;
(2)画出将△ABC先向上平移5个单位,再向右平移3个单位后所对应的△A1B1C1.并写出△A1B1C1的各顶点坐标;
(3)将点C’向上平移
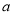 个单位后,点C’恰好落在△A1B1C1内,请你写出符合条件的一个整数
个单位后,点C’恰好落在△A1B1C1内,请你写出符合条件的一个整数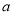 .(直接写出答案)
.(直接写出答案)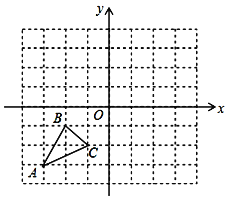
相关试题

