【题目】如图所示,写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标,并画出△ABC关于y对称的△A2B2C2.并求△ABC的面积。

参考答案:
【答案】A(﹣3,2),B(﹣4,-3),C(﹣1,-1),A1(﹣3,﹣2),B1(﹣4,3),C1(﹣1,1),作图见解析,△ABC的面积是![]() .
.
【解析】(1)根据图形关于y轴的对称特点,找出相应的点,把相应的点连接起来即可;
(2)分别求出各点的坐标,利用梯形的面积公式求解.
解:△ABC各顶点的坐标以及△ABC关于x轴对称的△A1B1C1的各顶点坐标:
A1(﹣3,﹣2),B1(﹣4,3),C1(﹣1,1),
如图所示:△A2B2C2,即为所求.

“点睛”此题主要考查了轴对称变换,正确掌握关于坐标轴对称点的性质是解题的关键.
解答此题要明确轴对称的性质:(1)对称轴是一条直线;(2)垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线.线段垂直平分线上的点到线段两端的距离相等;(3)在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等;(4)在轴对称图形中,对称轴把图形分成完全相等的两份;(5)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=
 的表达式;
的表达式;(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于x的单项式,探究其规律:2x,4x2 , 6x3 , 8x4 , 10x5 , 12x6 , …,按照上述规律,第2016个单项式是( )
A.2016x2015
B.2016x2016
C.4032x2015
D.4032x2016 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中B(3,2),BC⊥y轴于C,BA⊥x轴于A,点E在线段AB上从B向A以每秒1个单位的速度运动,运动时间为t秒(0<t<2).将BE沿BD折叠,使E点恰好落在BC上的F处.
(1)如图1,若E为AB的中点,请直接写出F、D两点的坐标:F( , ) D( , )
(2)如图1,连接CD,在(1)的条件下,求证:CD=FD.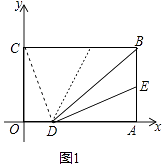
(3)如图2,在E点运动的同时,M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位.在运动过程中,△CMF能与△ANE全等吗?若能,求出此时a与t的值,若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E在AB上,且BE=
 AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
①FG= EH;②△DFE是直角三角形;③FG=
EH;②△DFE是直角三角形;③FG=  DE;④DE=EB+BC.
DE;④DE=EB+BC.
其中正确结论的个数是( )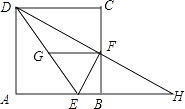
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以菱形AOBC的顶点O为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB=5,点C的坐标为(8,0),则点A的坐标为

-
科目: 来源: 题型:
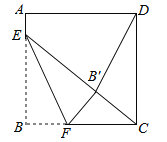
查看答案和解析>>【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′ 恰为等腰三角形,则DB′ 的长为 .
相关试题

