【题目】“五一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.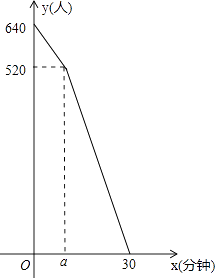
(1)求a的值.
(2)求检票到第20分钟时,候车室排队等候检票的旅客人数.
(3)若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?
参考答案:
【答案】
(1)
解:由图象知,640+16a﹣2×14a=520,
∴a=10
(2)
解:设当10≤x≤30时,y与x之间的函数关系式为y=kx+b,由题意,得
![]() ,
,
解得: ![]() ,
,
y=﹣26x+780,当x=20时,
y=260,
即检票到第20分钟时,候车室排队等候检票的旅客有260人
(3)
解:设需同时开放n个检票口,则由题意知
14n×15≥640+16×15
解得:n≥4 ![]() ,
,
∵n为整数,
∴n最小=5.
答:至少需要同时开放5个检票口
【解析】(1)根据原有的人数﹣a分钟检票额人数+a分钟增加的人数=520建立方程求出其解就可以;(2)设当10≤x≤30时,y与x之间的函数关系式为y=kx+b,由待定系数法求出函数的解析式,再将x=20代入解析式就可以求出结论;(3)设需同时开放n个检票口,根据原来的人数+15分进站人数≤n个检票口15分钟检票人数建立不等式,求出其解即可.
-
科目: 来源: 题型:
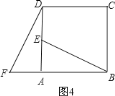
查看答案和解析>>【题目】如图,E、F是平行四边形ABCD对角线AC上两点,AE=CF.
证明(1)△ABE≌△CDF;
(2)BE∥DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图
 ,把
,把 沿直线
沿直线 平行移动线段
平行移动线段 的长度,可以变到
的长度,可以变到 的位置;
的位置;如图
 ,以
,以 为轴,把
为轴,把 翻折
翻折 ,可以变到
,可以变到 的位置;
的位置;如图
 ,以点
,以点 为中心,把
为中心,把 旋转
旋转 ,可以变到
,可以变到 的位置.
的位置.像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图
 中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使
中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使 变到
变到 的位置;
的位置;②指图中线段
 与
与 之间的关系,为什么?
之间的关系,为什么?
-
科目: 来源: 题型:
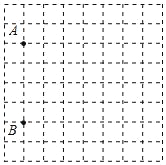
查看答案和解析>>【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:
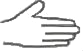 ﹣3x=x2﹣5x+1
﹣3x=x2﹣5x+1(1)求所捂的二次三项式;
(2)若x=
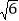 +1,求所捂二次三项式的值;
+1,求所捂二次三项式的值;(3)如果
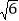 +1的整数部分为a,则a2= .
+1的整数部分为a,则a2= . -
科目: 来源: 题型:
查看答案和解析>>【题目】
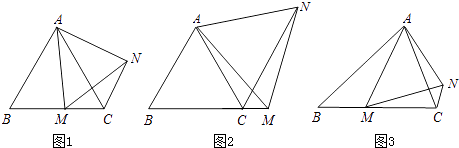
(1)【提出问题】
如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
(2)【类比探究】
如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
(3)【拓展延伸】
如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
相关试题

