【题目】已知直线y=kx+b经过A(0,2),B(4,0)两点.
(1)求直线AB对应的函数解析式;
(2)将该直线向上平移6个单位,求平移后的直线与x轴交点的坐标.
参考答案:
【答案】(1)y=-![]() x+2(2)(16,0)
x+2(2)(16,0)
【解析】
(1)将两点代入即可求出k和b的值,继而可得出答案;
(2)根据上加下减的法则可得出平移后的解析式,令y=0可求出与x轴交点的坐标.
(1)将A(0,2),B(4,0)的坐标代入y=kx+b,
可得![]() 解得
解得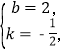
∴y=-![]() x+2;
x+2;
(2)将直线y=-![]() x+2向上平移6个单位,即得到直线y=-
x+2向上平移6个单位,即得到直线y=-![]() x+8,
x+8,
当y=0时,有-![]() x+8=0,解得x=16,即直线y=-
x+8=0,解得x=16,即直线y=-![]() x+8与x轴交点是(16,0),
x+8与x轴交点是(16,0),
所以平移后的直线与x轴交点的坐标为(16,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
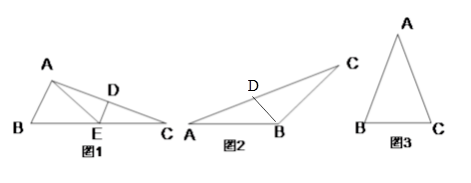
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.
求证:AE是△ABC的一条特异线.
(2)如图2,已知BD是△ABC的一条特异线,其中∠A=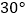 ,∠ABC为钝角,求出所有可能的∠ABC的度数.
,∠ABC为钝角,求出所有可能的∠ABC的度数.
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角
度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数. -
科目: 来源: 题型:
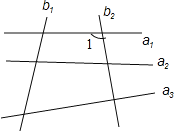
查看答案和解析>>【题目】如图,直线a1、a2、a3分别与直线b1、b2相交,与∠1构成同位角的角共有________个,和∠l构成内错角的角共有________个,与∠1构成同旁内角的角共有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与
与  轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与  轴交于点C(0,-3),顶点为D。
轴交于点C(0,-3),顶点为D。
(1)求抛物线的解析式及顶点D的坐标。
(2)联结AC,BC,求∠ACB的正切值。
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由。
(4)M是抛物线上一点,点N在 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( )
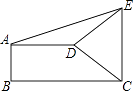
A.1
B.2
C.3
D.4
相关试题

