Question

【题目】如图，在平面直角坐标系xOy中，点O为坐标原点，直线y＝－x＋4与x轴交于点A，与y轴交于点B.

(1)求点A，B的坐标；

(2)在直线AB上是否存在点P，使△OAP是以OA为底边的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由；

(3)若将Rt△AOB折叠，使OB边落在AB上，点O与点D重合，折痕为BC，求点C的坐标。

(4)直接写出折痕BC所在直线的表达式．

Answer 1

【答案】(1) A(4,0),B(0,4)； (2) P点坐标为(2,2)； (3) C(44,0)；(4) 折痕BC的解析式为y=-(1+)x+4.

【解析】

（1）利用直线解析式，容易求得A、B的坐标；
（2）作线段OA的垂直平分线，交x轴于点E，交AB于点P，则P点即为所求，可求得E点坐标，则容易求得P点坐标；
（3）可设C（t，0），由折叠的性质可得到CD=t，AC=4-t，在Rt△ACD中，由勾股定理可得到关于t的方程，可求得t的值，则可求得C点坐标；

（4）利用待定系数法可求得直线BC的解析式．

解：(1)在y=x+4中，令x=0可得y=4，令y=0可求得x=4，

∴A(4,0)，B(0,4)；

(2)如图1，作线段OA的垂直平分线，交x轴于点E，交AB于点P，

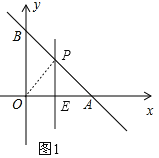
则OP=PA，即P点即为满足条件的点，

∵OA=4，

∴OE=2，

在y=x+4中，当x=2时，可得y=2，

∴P点坐标为(2,2)；

(3)设C(t,0)，则AC=OAOC=4t，

∵OA=OB=4，

∴AB=4，

由折叠的性质可得BD=OB=4,CD=OC=t,∠ADC=∠BOC=90，

∴AD=ABBD=44，

在Rt△ACD中，由勾股定理可得AC2=AD2+CD2,即(4t)2=t2+(44)2,

解得t=44，

∴C(44,0)，

(4) 设直线BC解析式为y=kx+b，

∵B(0,4)，C(44,0)

∴

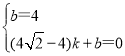
解得：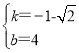

折痕BC的解析式为y=-(1+)x+4