【题目】(1)先化简,再求值:已知代数式A=(3a2b﹣ab2),B=(﹣ab2+3a2b),求5A﹣4B,并求出当a=﹣2,b=3时5A﹣4B的值.
(2)对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).规定:(a,b)★(c,d)=ad﹣bc,如:(1,2)★(3,4)=1×4﹣2×3=﹣2
根据上述规定解决下列问题:
①有理数对(5,﹣3)★(3,2)= .
②若有理数对(﹣3,x)★(2,2x+1)=15,则x= .
③若有理数对(2,x﹣1)★(k,2x+k)的值与x的取值无关,求k的值.
参考答案:
【答案】(1)54;(2)①19,②﹣![]() ,③4
,③4
【解析】
(1)把A与B代入5A﹣4B中,去括号合并得到最简结果,把a与b的值代入计算即可求出值;
(2)①原式根据题中的新定义计算即可求出值;
②原式根据题中的新定义计算即可求出值;
③原式根据题中的新定义计算即可求出值.
解:(1)∵A=(3a2b﹣ab2),B=(﹣ab2+3a2b),
∴5A﹣4B=5(3a2b﹣ab2)﹣4(﹣ab2+3a2b)=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2,
当a=﹣2,b=3时,原式=36+18=54;
(2)①根据题中的新定义得:原式=10+9=19;
②根据题中的新定义得:﹣3(2x+1)﹣2x=15,
去括号得:﹣6x﹣3﹣2x=15,
移项合并得:﹣8x=18,
解得:x=﹣![]() ;
;
③根据题中的新定义化简得:2(2x+k)﹣k(x﹣1)=4x+2k﹣kx+k=(4﹣k)x+3k,
由结果与x取值无关,得到4﹣k=0,即k=4.
故答案为:①19;②﹣![]() ;③4
;③4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是
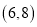 ,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.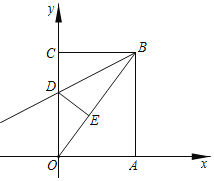
(1)求直线OB的解析式及线段OE的长;
(2)求直线BD的解析式及点E的坐标;
(3)若点P是平面内任意一点,点M是直线BD上的一个动点,过点M作
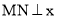 轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第6个图形的小圆个数是( )

A. 56 B. 54 C. 44 D. 42
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,
一般情况下走路线二的平均车速是走路线一的平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.那么走路线二的平均车速是每小时多少千米?
-
科目: 来源: 题型:
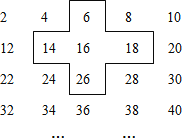
查看答案和解析>>【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在日历中移动的规律后,突发奇想,将连续的得数2,4,6,8,…,排成如图形式:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)请你选择十字框中你喜欢的任意位置的一个数,将其设为x,并用含x的代数式表示十字框中五个数的和.
(2)若将十字框上下左右移动,可框住另外的五个数,试间:十字框能否框住和等于2015的五个数,如能,请求出这五个数;如不能,说明理由.
-
科目: 来源: 题型:
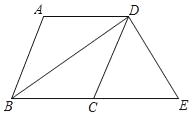
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,3).
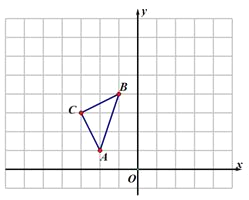
(1)画出△ABC绕点B逆时针旋转90°得到的△A1BC1.
(2)以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△ABC放大后的△A2B2C2,并写出A2点的坐标_________.
相关试题

