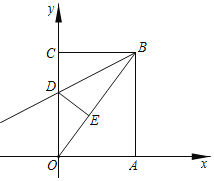
【题目】如图,矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是![]() ,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
(1)求直线OB的解析式及线段OE的长;
(2)求直线BD的解析式及点E的坐标;
(3)若点P是平面内任意一点,点M是直线BD上的一个动点,过点M作![]() 轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,OE=4;(2)
,OE=4;(2)![]() ,
,![]() ;(3)存在,点M的坐标为
;(3)存在,点M的坐标为![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
![]() 利用待定系数法求出k,再利用勾股定理求出OB,由折叠求出
利用待定系数法求出k,再利用勾股定理求出OB,由折叠求出![]() ,即可得出结论;
,即可得出结论;
![]() 利用勾股定理求出点D坐标,利用待定系数法求出直线BD的解析式,最后用三角形的面积公式求出点E的横坐标,即可得出结论;
利用勾股定理求出点D坐标,利用待定系数法求出直线BD的解析式,最后用三角形的面积公式求出点E的横坐标,即可得出结论;
![]() 分两种情况,利用菱形的性质求出点N坐标,进而得出点M的横坐标,代入直线BD解析式中,即可得出结论.
分两种情况,利用菱形的性质求出点N坐标,进而得出点M的横坐标,代入直线BD解析式中,即可得出结论.
解:![]() 设直线OB的解析式为
设直线OB的解析式为![]() ,
,
将点![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() ,
,
![]() 直线OB的解析式为
直线OB的解析式为![]() ,
,
![]() 四边形OABC是矩形,且
四边形OABC是矩形,且![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
根据勾股定理得,![]() ,
,
由折叠知,![]() ,
,
![]() ;
;
![]() 设
设![]() ,
,
![]() ,
,
由折叠知,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
根据勾股定理得,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
设直线BD的解析式为![]() ,
,
![]() ,
,
∴6k`+5=8
∴K`=![]()
![]() 直线BD的解析式为
直线BD的解析式为![]() ,
,
由![]() 知,直线OB的解析式为
知,直线OB的解析式为![]() ,
,
设点![]() ,
,
根据![]() 的面积得,
的面积得,![]() ,
,
![]() ,
,
![]() ;
;
![]() 由
由![]() 知,
知,![]() ,
,
![]() 以P、N、E、O为顶点的四边形是菱形,
以P、N、E、O为顶点的四边形是菱形,
![]() 当OE是菱形的边时,
当OE是菱形的边时,![]() ,
,
![]() 或
或![]() ,
,
Ⅰ、当![]() 时,
时,
![]() 轴,
轴,
![]() 点M的横坐标为4,
点M的横坐标为4,
![]() 点M是直线BD:
点M是直线BD:![]() 上,
上,
![]() ,
,
Ⅱ、当![]() 时,
时,
![]() 轴,
轴,
![]() 点M的横坐标为
点M的横坐标为![]() ,
,
![]() 点M是直线BD:
点M是直线BD:![]() 上,
上,
![]() ,
,
![]() 当OE是菱形的对角线时,记对角线的交点为
当OE是菱形的对角线时,记对角线的交点为![]() ,
,![]() ,
,
由![]() 知,
知,![]() ,
,
![]() ,
,
由![]() 知,直线OB的解析式为
知,直线OB的解析式为![]() ,
,
![]() 点
点![]() 过直线PN,
过直线PN,
![]() 直线PN的解析式为
直线PN的解析式为![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() 点M的横坐标为
点M的横坐标为![]() ,
,
![]() 点M是直线BD:
点M是直线BD:![]() 上,
上,
![]() ,
,
当ON为对角线时,ON与EP互相平分,
![]() 点
点![]() ,
,
![]() ;
;
即:点M的坐标为![]() 或
或![]() 或
或![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①两个数互为倒数,则它们乘积为1;②若a、b互为相反数,则
 =﹣1;③两个四次单项式的和一定是四次多项式;④两个有理数比较,绝对值大的反而小;⑤若a为任意有理数,则a﹣|a|≤0;⑥﹣5πR2的系数是﹣5.其中正确的有( )
=﹣1;③两个四次单项式的和一定是四次多项式;④两个有理数比较,绝对值大的反而小;⑤若a为任意有理数,则a﹣|a|≤0;⑥﹣5πR2的系数是﹣5.其中正确的有( )A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AMAD;③MN=3-
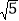 ;④S△EBC=2
;④S△EBC=2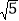 -1,其中正确的结论是_________(把你认为正确结论的序号都填上).
-1,其中正确的结论是_________(把你认为正确结论的序号都填上).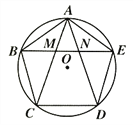
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第6个图形的小圆个数是( )

A. 56 B. 54 C. 44 D. 42
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,
一般情况下走路线二的平均车速是走路线一的平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.那么走路线二的平均车速是每小时多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:已知代数式A=(3a2b﹣ab2),B=(﹣ab2+3a2b),求5A﹣4B,并求出当a=﹣2,b=3时5A﹣4B的值.
(2)对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).规定:(a,b)★(c,d)=ad﹣bc,如:(1,2)★(3,4)=1×4﹣2×3=﹣2
根据上述规定解决下列问题:
①有理数对(5,﹣3)★(3,2)= .
②若有理数对(﹣3,x)★(2,2x+1)=15,则x= .
③若有理数对(2,x﹣1)★(k,2x+k)的值与x的取值无关,求k的值.
相关试题

