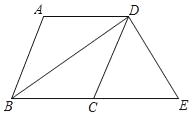
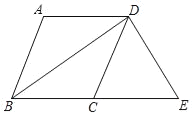
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
参考答案:
【答案】(1)详见解析;(2)26.
【解析】
(1)根据平行线的性质得到∠ADB=∠CBD,根据角平分线定义得到∠ABD=∠CBD,等量代换得到∠ADB=∠ABD,根据等腰三角形的判定定理得到AD=AB,根据菱形的判定即可得到结论;
(2)由垂直的定义得到∠BDE=90°,等量代换得到∠CDE=∠E,根据等腰三角形的判定得到CD=CE=BC,根据勾股定理得到DE=![]() =6,于是得到结论.
=6,于是得到结论.
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵BA=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,
∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,
∴∠DBC=∠BDC,
∴∠CDE=∠E,
∴CD=CE=BC,
∴BE=2BC=10,
∵BD=8,
∴DE=![]() =6,
=6,
∵四边形ABCD是菱形,
∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,
一般情况下走路线二的平均车速是走路线一的平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.那么走路线二的平均车速是每小时多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:已知代数式A=(3a2b﹣ab2),B=(﹣ab2+3a2b),求5A﹣4B,并求出当a=﹣2,b=3时5A﹣4B的值.
(2)对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).规定:(a,b)★(c,d)=ad﹣bc,如:(1,2)★(3,4)=1×4﹣2×3=﹣2
根据上述规定解决下列问题:
①有理数对(5,﹣3)★(3,2)= .
②若有理数对(﹣3,x)★(2,2x+1)=15,则x= .
③若有理数对(2,x﹣1)★(k,2x+k)的值与x的取值无关,求k的值.
-
科目: 来源: 题型:
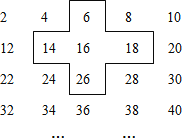
查看答案和解析>>【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在日历中移动的规律后,突发奇想,将连续的得数2,4,6,8,…,排成如图形式:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)请你选择十字框中你喜欢的任意位置的一个数,将其设为x,并用含x的代数式表示十字框中五个数的和.
(2)若将十字框上下左右移动,可框住另外的五个数,试间:十字框能否框住和等于2015的五个数,如能,请求出这五个数;如不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,3).
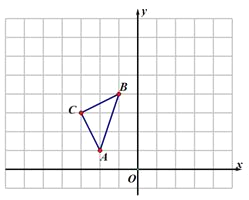
(1)画出△ABC绕点B逆时针旋转90°得到的△A1BC1.
(2)以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△ABC放大后的△A2B2C2,并写出A2点的坐标_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,②分别是某吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角. 吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A距地面的高度是多少米?(精确到0.1米. 参考数据:sin10°=cos80°≈0.17,cos10°=sin80°≈0.98,sin20°=cos70°≈0.34,tan70°≈2.75,sin70°≈0.94)
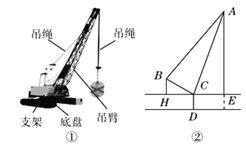
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,今年云南省面向县级及农村地区推广,为相应号召,某商场计划用3800元购进节能灯120只,这两种节能灯的进价、售价如下表:

(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
相关试题

