【题目】某物流公司的快递车和货车同时从甲地出发,匀速向乙地行驶,快递车的速度为100km/h,货车的速度为60km/h,结果快递车比货车早2h到达乙地.快递车到达乙地后卸完物品再另装货物共用30min,立即按原路以90km/h速度匀速返回,直至与货车相遇.设两车之间的距离y(km).货车行驶时间为x(h).
(1)求甲、乙两地之间的距离.
(2)求快递车返回时y与x之间的函数关系式.
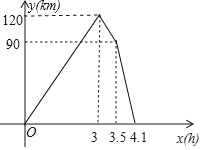
(3)建立适当的坐标系画出y与x之间的函数图象.
参考答案:
【答案】(1)300km;(2)y=﹣150x+615(3![]() ≤x≤4
≤x≤4![]() ).(3)见解析.
).(3)见解析.
【解析】试题分析:(1)设甲、乙两地之间的距离为skm,根据时间=路程÷速度结合快递车比货车早2h到达乙地,即可得出关于s的一元一次方程,解之即可得出结论;
(2)先求出快递车离开乙地的时间以及此时两车间的距离,再根据路程=初始距离-两车速度和×行驶时间,即可得出快递车返回时y与x之间的函数关系式,找出x的取值范围,此题得解;
(3)找出当x=3时,y的值,由此可得出函数图象上的各节点坐标,描点、连线,即可画出函数图象.
解:(1)设甲、乙两地之间的距离为skm,
根据题意得:![]() ﹣
﹣![]() =2,
=2,
解得:s=300.
答:甲、乙两地之间的距离为300km.
(2)快递车达到乙地的时间为300÷100=3(h),
快递车离开乙地的时间为3+![]() =3
=3![]() (h),
(h),
快递车离开乙地时,两车间的距离为300﹣60×3![]() =90(km),
=90(km),
两车相遇的时间为3![]() +90÷(60+90)=4
+90÷(60+90)=4![]() (h).
(h).
∴快递车返回时y与x之间的函数关系式为y=90﹣(60+90)(x﹣3.5)=﹣150x+615(3![]() ≤x≤4
≤x≤4![]() ).
).
(3)当x=3时,两车间的距离为300﹣60×3=120(km),
∴函数图象上各节点坐标为(0,0)、(3,120)、(3.5,90)、(4.1,0).
画出函数图象,如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D、E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,CD=2,则DF的长为( )
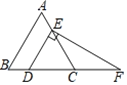
A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).【参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42,
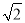 =1.41】
=1.41】
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线EF//MN,点A、B分别为EF,MN上的动点,且∠ACB= a,BD平分∠CBN交EF于D.
(1)若∠FDB=120°,a=90°.如图1,求∠MBC与∠EAC的度数?
(2)延长AC交直线MN于G,这时a =80°,如图2,GH平分∠AGB交DB于点H,问∠GHB是否为定值,若是,请求值.若不是,请说明理由?


-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4,点D是AB的中点,动点P、Q同时从点D出发(点P、Q不与点D重合),点P沿D→A以1cm/s的速度向中点A运动.点Q沿D→B→D以2cm/s的速度运动.回到点D停止.以PQ为边在AB上方作正方形PQMN,设正方形PQMN与△ABC重叠部分的面积为S(cm2),点P运动的时间为t(s).
(1)当点N在边AC上时,求t的值.
(2)用含t的代数式表示PQ的长.
(3)当点Q沿D→B运动,正方形PQMN与△ABC重叠部分图形是五边形时,求S与t之间的函数关系式.
(4)直接写出正方形PQMN与△ABC重叠部分图形是轴对称图形时t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,若MN=2,则NF=___________

相关试题

