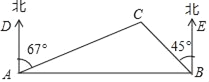
【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).【参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42, ![]() =1.41】
=1.41】
参考答案:
【答案】5.5海里
【解析】试题分析:本题考查了解直角三角形的应用---方向角问题,作CD⊥AB,在Rt△ADC中由sin23°=![]() ,求得CD=3.9,在Rt△BCD中由sin45°=
,求得CD=3.9,在Rt△BCD中由sin45°=![]() ,求得BC=
,求得BC=![]() CD,即可得出答案.
CD,即可得出答案.
解:过点C作CD⊥AB于点D,

由题意,得:∠BAC=23°,∠ABC=45°,AC=10,
在Rt△ADC中,∠ADC=90°,
∴sin23°=![]() =0.39,
=0.39,
∴CD=10×0.39=3.9,
在Rt△BCD中,∠CDB=90°,
∴sin45°=![]() =
=![]() ,
,
∴BC=![]() CD=1.41×3.9=5.499≈5.5,
CD=1.41×3.9=5.499≈5.5,
答:码头B与小岛C的距离是5.5海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.

-
科目: 来源: 题型:
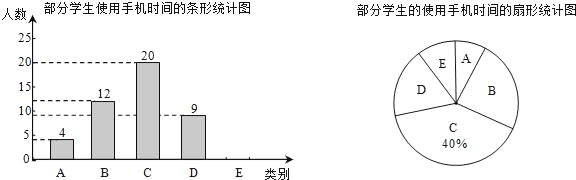
查看答案和解析>>【题目】随着手机普及率的提高,有些人开始过分依赖手机,一天中使用手机时间过长而形成了“手机瘾”,某校学生会为了了解本校初三年级的手机使用情况,随机调查了部分学生的手机使用时间,将调查结果分成五类:
A、基本不用;B、平均每天使用1~2h;C、平均每天使用2~4h;D、平均每天使用4~6h;E、平均每天使用超过6h,并根据统计结果绘制成了如下两幅不完整的统计图.
(1)学生会一共调查了多少名学生?
(2)此次调查的学生中属于E类的学生有 人,并补全条形统计图;
(3)若一天中手机使用时间超过6h,则患有严重的“手机瘾”,该校初三学生共有900人,请估计该校初三年级中患有严重的“手机瘾”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D、E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,CD=2,则DF的长为( )
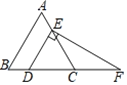
A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线EF//MN,点A、B分别为EF,MN上的动点,且∠ACB= a,BD平分∠CBN交EF于D.
(1)若∠FDB=120°,a=90°.如图1,求∠MBC与∠EAC的度数?
(2)延长AC交直线MN于G,这时a =80°,如图2,GH平分∠AGB交DB于点H,问∠GHB是否为定值,若是,请求值.若不是,请说明理由?


-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司的快递车和货车同时从甲地出发,匀速向乙地行驶,快递车的速度为100km/h,货车的速度为60km/h,结果快递车比货车早2h到达乙地.快递车到达乙地后卸完物品再另装货物共用30min,立即按原路以90km/h速度匀速返回,直至与货车相遇.设两车之间的距离y(km).货车行驶时间为x(h).
(1)求甲、乙两地之间的距离.
(2)求快递车返回时y与x之间的函数关系式.
(3)建立适当的坐标系画出y与x之间的函数图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
相关试题

