【题目】如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,若MN=2,则NF=___________

参考答案:
【答案】1
【解析】
连接AN、AM,根据等腰三角形性质可知∠B=∠C=30°,利用线段垂直平分线定理可得BM=AM,AN=CN,根据等边对等角可知∠B=∠MAB,∠NAC=∠C,即可知道△AMN是等边三角形,进而得到AN的长,利用直角三角形中30°角所对的直角边是斜边的一半,即可求得NF的长.
如图,连接AN、AM,
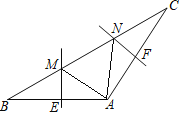
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵ME、NF分别垂直平分线段AB、AC
∴BM=AM,AN=CN,
∴∠B=∠MAB=30°,∠NAC=∠C=30°,
∴∠AMN=∠MAN=∠MNA=60°
∴△AMN是等边三角形,
∴AN=MN=2
在Rt△ANF中,∠NAF=30°
∴NF=![]() AN=1
AN=1
故答案为:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司的快递车和货车同时从甲地出发,匀速向乙地行驶,快递车的速度为100km/h,货车的速度为60km/h,结果快递车比货车早2h到达乙地.快递车到达乙地后卸完物品再另装货物共用30min,立即按原路以90km/h速度匀速返回,直至与货车相遇.设两车之间的距离y(km).货车行驶时间为x(h).
(1)求甲、乙两地之间的距离.
(2)求快递车返回时y与x之间的函数关系式.
(3)建立适当的坐标系画出y与x之间的函数图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4,点D是AB的中点,动点P、Q同时从点D出发(点P、Q不与点D重合),点P沿D→A以1cm/s的速度向中点A运动.点Q沿D→B→D以2cm/s的速度运动.回到点D停止.以PQ为边在AB上方作正方形PQMN,设正方形PQMN与△ABC重叠部分的面积为S(cm2),点P运动的时间为t(s).
(1)当点N在边AC上时,求t的值.
(2)用含t的代数式表示PQ的长.
(3)当点Q沿D→B运动,正方形PQMN与△ABC重叠部分图形是五边形时,求S与t之间的函数关系式.
(4)直接写出正方形PQMN与△ABC重叠部分图形是轴对称图形时t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作CPBD,设CPBD的面积为S,点P的横坐标为m.
(1)求抛物线对应的函数表达式;
(2)当点P在第四象限,且CPBD有两个顶点在x轴上时,求点P的坐标;
(3)求S与m之间的函数关系式;
(4)当x轴将CPBD的面积分成1:7两部分时,直接写出m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式组:
(1)
 ;
;(2)
 ;
;(3)
 ;
;(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.

相关试题

