【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am-b).
其中所有正确的结论是( )
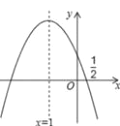
A. ①②③ B. ①③④ C. ①②③⑤ D. ①③⑤
参考答案:
【答案】D
【解析】试题分析:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣![]() =﹣1,可得b=2a,
=﹣1,可得b=2a,
a﹣2b+4c=a﹣4a+4c=﹣3a+4c,
∵a<0,
∴﹣3a>0,
∴﹣3a+4c>0,
即a﹣2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(﹣![]() ,0),
,0),
当x=﹣![]() 时,y=0,即a(﹣
时,y=0,即a(﹣![]() )2+b×(﹣
)2+b×(﹣![]() )+c=0,
)+c=0,
整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴![]() b+b+c<0,
b+b+c<0,
即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,
∴a﹣b+c>m2a﹣mb+c(m≠1),
∴a﹣b>m(am﹣b),所以⑤正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=-x+4的图象与反比例
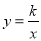 (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)连接OA,OB,求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市从
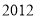 年
年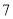 月
月 日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)档次
全年的用电量
电价(单位:元/度)
第一档
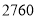 度以内(包括
度以内(包括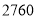 度)
度)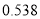
第二档
 至
至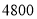 度(包含
度(包含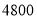 度)
度)
第三档
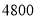 度以上
度以上
(
 )小王家
)小王家 年全年的用电量是
年全年的用电量是 度,请计算小王家这年的电费付了多少元?
度,请计算小王家这年的电费付了多少元?(
 )小李家
)小李家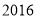 年
年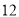 月份这个月的用电量是
月份这个月的用电量是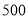 度,小李算出它们家的电费是
度,小李算出它们家的电费是 元,而供电局却收了小李家的电费
元,而供电局却收了小李家的电费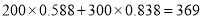 元,你知道其中的奥秘吗?请你来解释下.
元,你知道其中的奥秘吗?请你来解释下.(
 )小张家
)小张家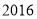 年全年用电量为
年全年用电量为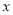 度,请用含
度,请用含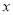 的代数式表示小张家全年应交的总电费,并把结果化简.
的代数式表示小张家全年应交的总电费,并把结果化简. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,A与D,B与E分别是对应顶点,∠A=52°,∠B=67°,BC=15cm,则∠F=________,FE=_________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个正五棱柱的底面边长为2cm,高为4cm。

(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有
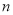 的代数式表示
的代数式表示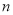 棱柱的顶点数、面数、与棱的条数。
棱柱的顶点数、面数、与棱的条数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=12
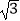 cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以2
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以2 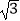 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s. 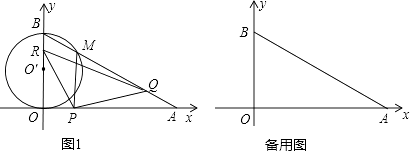
(1)求∠OAB的度数.
(2)以OB为直径的⊙O′与AB交于点M,当t为何值时,PM与⊙O′相切?
(3)是否存在△RPQ为等腰三角形?若存在,请直接写出t值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2x2﹣5x+3的图象与x轴的交点有( )
A.1个B.2个C.3个D.4个
相关试题

